培养学生空间想象能力的几点看法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-5-25 阅读:36411次 |
||
培养学生空间想象能力的几点看法 绥宁一中 邓成林 认识空间图形,培养和发展学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力,以及几何直观能力,是高中阶段数学课程的基本要求,学生通过学习立体几何,可以更好地认识和理解人类生存的空间,发展直觉能力,增强探究的好奇心,从而激发出潜在的创造力,形成创新意识。但初学立体几何的学生空间想象力薄弱,还停留在平面几何的认识上,不懂得按题意画出空间图形,或画出的图形不直观造成解题困难。如何对学生进行学法指导,使他们能尽快更好学好立体几何。我结合自己的教学实践谈几点看法,供大家参考。 一、发挥直观的几何模型的作用,培养空间想象力。 从具体到抽象是人们正确认识客观事物的一个阶段,初学立体几何应给学生 观察各种实物模型,除用多媒体演示外,还应指导学生制造许多常用的小型模具,如空间四边形、正三棱锥、正方体等。尤其是正方体模型,因为它对立体几何中线线、线面、面面等关系和性质,都能很清楚地反映出来,容易理解,对培养学生空间想象能力起到很重要的作用。例如在正方体模型中用细线将A1、C连接,结合图形,要求学生指出和对角线A1C成异面直线的有哪几条?每个学生都能对图形与实物相对照,准确找出所有直线,这样活用正方体模型可加深学生认识,丰富他们的想象力。再如:三个面在空间中的各种位置情况,可以引导学生用硬纸片作模型摆出各种不同的可能空间位置,侧面是全等的等腰三角形的棱锥是否正棱锥,可以用硬纸片制作棱锥;学习三垂线定理时,引导学生用三角板构造垂线、斜线、射影。这样学生在平时学习中也经常借助正方体等模型去观察考虑有关问题,加深对线线、线面、面面关系及有关性质的理解,培养学生空间想象力。 二、培养学生识图、绘图能力,发展空间想象力。
再如:正方形ABCD-A1B1C1D1中,棱AA1=1,M为BB1的中点,求△AMC1所在平面与平面ABCD所成二面角的余弦值。图(2)的位置选择得不当,四边形AMC1N几乎变成一条线,观察图形AMC1N是菱形很困难。而图(3)的图形位置好,直观性强,学生很容易证明出AMC1N是菱形,因此容易想到
三、适当运用多媒体演示,培养空间想象力。
再如,在讲解三棱锥的体积时,可以演示将三棱柱分割成三个体积相等的三棱锥的过程,如图(5)所示,利用几何画板虚拟实验情境,演示更接近于基本图形的切拼过程,再结合必要的解说使学生更深刻地理解了三棱锥公式的推导过程,同时通过启发性提问,引导学生积极开展思维,自我挖掘各图形间的内在联系以及有关计算公式的推出又如, 在学习旋转体知识时,可以通过课件动态演示:平面图形旋转一周形成的立体图形,让学生体验平面与立体图形的联系,既巩固了所学又拓展了思路,进一步培养学生的空间想象能力。而这一旋转过程用传统教具是无法演示生成的,计算机则展示出了她神奇的魅力,动画模拟不但能彻底改变传统教学中的凭空想象、似有非有、难以理解之苦,同时还能充分激发学生学习主观能动性,化被动为主动,产生特有的教学效果。 三、精选例题,培养空间想象能力。 正确选择例题和习题对培养空间想象能力,发展智力很重要,要注意选一些能善于利用空间观念,富思考性的问题,帮助学生弄清有关慨念,提高识图能力。 例1、
这些问题不难,但却可以把线线、线面、面面各种关系包含在其中,要求学生有较强的空间想象力。
思路1、采用直接法先确定底面形状和高,再计算底面积和高 把△ABC视作底面,∵∠BAC=60°,AB=AC=2a,∴△ABC是边长为2a的正方形,∴ 即
(2)连结PD,易知,
可得 若注意到PA⊥面PBC,高可视为PA,底面视为等腰三角形PBC,于是就有优于解法1的思路。 解法2:依题意∠PAB=60°,PA=a,AB=2a,故∠APB=90°,同理∠APC=90°,∴ PA⊥面PBC,而
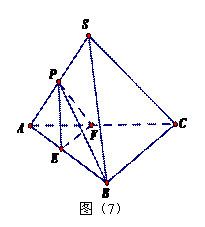
以上两种解法都有意无意地运用了截面PAD,没有对图形的整体结构有较好的认识,看到截面PAD,必能想到BC⊥面PAD,且D为BC的中点,△PAD为直角三角形,于是又会想到以下解法。 解法3:设D 为BC的中点,依题意有AP⊥PD, BC⊥面PAD, 解法4:设E,F分别是AB与AC的中点,连结PE,PF,EF,如图(6),易知三棱锥P-AEF是棱长为a的正四面体,并且三棱锥P-AEF与三棱锥P-ABC等高,易得
讲完解法4后引导学生分析,既然能分割,是否可补形呢?考虑到从A出发的三条棱两两的夹角为60°,故可补形为正四面体,得出如下解法: 解法5:如图(7),延长AP至S,使PA=PS,连结SB,SC,得到边长为2a的正四面体,而且 以上五种解法一种比一种简单,要想到较好的解法必须有较好的空间想象能力,对空间图形要有一个较透彻的认识。 讲完该例后可让学生做如下变式练习:如图,正方体 例3 、已知:(条件1)四边形ABCD是空间四边形(四个顶点不共面的四边形),(条件2)E、H分别是AB、AD的中点,(条件3)F、G分别是边CB、CD上的点,且 在讲解这个例题时先要求学生画出满足条件2、3的平面图形ABCD,再将平面图形沿BD翻折满足条件1(目的是让学生区别平面四边形和空间四边形);讲完后让学生思考: 变式1:已知四边形ABCD是空间四边形(四个顶点不共面的四边形),E、H、G、H分别是边AB、AD、CD 、CB上的点,问 变式2:已知四边形ABCD是空间四边形(四个顶点不共面的四边形),E、H、G、H分别是边AB、AD、CD 、CB上的点,且 变式3:已知四边形ABCD是空间四边形(四个顶点不共面的四边形),E、H、G、H分别是边AB、AD、CD 、CB上的点,且 总之,在立体几何里培养学生空间想象能力的载体很多,诸如:证明空间的线面、线线、面面的平行、垂直,计算空间的有关距离、角度、面积、体积等等,只有对几何图形的空间整体结构有了正确而牢固地把握,才能在这些载体的依托下充分展现空间想象能力。一般地,在解(证)立体几何题时,先把条件分类,然后标在图上,使题目和图形分离开来,看图形,想象空间结构,把多面体每个面都“拆”下来,再“安装”复位;把空间的所有平行、垂直关系牢牢印记在脑海里;把空间图形“切割”成几小块,然后“安装”复位;把空间图形补全后,再取出来,这些过程必须通过一定的解题实践,如能经常依托各种载体进行空间结构想象的训练,空间想象能力一定会明显提高。 (此文在2011年参评湖南省教育协会论文大赛获壹等奖) |
||
- 上一篇:论如何开发“潜能生”的潜能
- 下一篇:谈谈在基础薄弱班级的英语教学
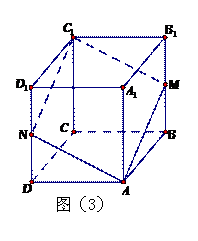 根据命题的条件能够画出准确地反映命题条件的立体几何直观图对于解题分析很有帮助。平时在教学中要加强画图的训练和指导,注意纠正学生常出现的错误画法。例如:O是正方形ABCD的中心,PO垂直平面ABCD,初学立体几何时学生易错画成图(1)这种情形;
根据命题的条件能够画出准确地反映命题条件的立体几何直观图对于解题分析很有帮助。平时在教学中要加强画图的训练和指导,注意纠正学生常出现的错误画法。例如:O是正方形ABCD的中心,PO垂直平面ABCD,初学立体几何时学生易错画成图(1)这种情形;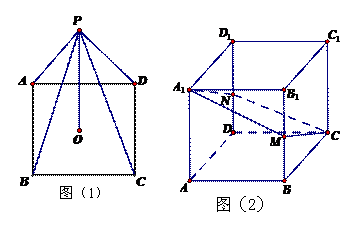
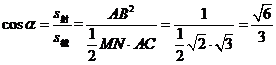 ,由此可看出图形位置选择很重要,图形选择不恰当,会影响解题分析。相反,图形位置选择的好,图形的直观性强,就有助于解题的分析。所以教师上课时要.即时画图,边引导边画图,让学生看到实际操作过程,或者让学生在练习本与教师同步绘制。千万不要把图形事先画在小黑板上。对于复杂图形,一方面图中点、线、面较多,影响观察、分析,另一方面由于是直观图,视觉上的感受容易引起理解上的错觉。我们可以把一部分图形,从整体图形中“肢解”出去,尤其是把在同一平面内的点、线画在一个平面图形中去研究,很容易把握住问题的本质。
,由此可看出图形位置选择很重要,图形选择不恰当,会影响解题分析。相反,图形位置选择的好,图形的直观性强,就有助于解题的分析。所以教师上课时要.即时画图,边引导边画图,让学生看到实际操作过程,或者让学生在练习本与教师同步绘制。千万不要把图形事先画在小黑板上。对于复杂图形,一方面图中点、线、面较多,影响观察、分析,另一方面由于是直观图,视觉上的感受容易引起理解上的错觉。我们可以把一部分图形,从整体图形中“肢解”出去,尤其是把在同一平面内的点、线画在一个平面图形中去研究,很容易把握住问题的本质。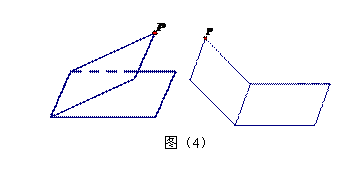 初学立体几何时大多数学生不具备丰富的想象力及较强的平面与空间图形的转化能力,主要原因是学生依靠对二维平面图形的直观来感知和想象三维空间图形,尤其是在平面上绘出立体图形时由于受到视角的影响很难画出准确的直观图,而利用多媒体信息技术可以使知识推导、学生的思考过程具体化、形象化,使学生感受知识形成过程,从而达到使学生领会、突破难点的目的。如在讲解二面角的定义时,利用几何画板画出如图(4)的图形,当拖动P点时,点P所在的半平面也随之转动,从而使学生直观感受二面角的大小的变化情况
初学立体几何时大多数学生不具备丰富的想象力及较强的平面与空间图形的转化能力,主要原因是学生依靠对二维平面图形的直观来感知和想象三维空间图形,尤其是在平面上绘出立体图形时由于受到视角的影响很难画出准确的直观图,而利用多媒体信息技术可以使知识推导、学生的思考过程具体化、形象化,使学生感受知识形成过程,从而达到使学生领会、突破难点的目的。如在讲解二面角的定义时,利用几何画板画出如图(4)的图形,当拖动P点时,点P所在的半平面也随之转动,从而使学生直观感受二面角的大小的变化情况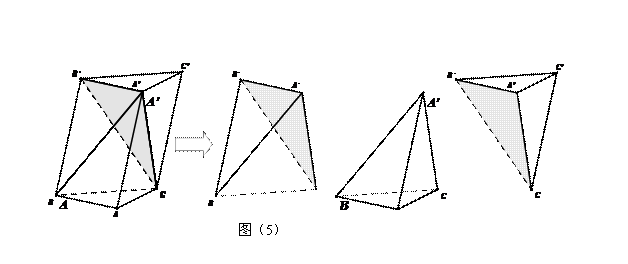
 例2、在三棱锥P-ABC中,AB=AC=2a,∠PAB=∠PAC=∠BAC=60°,求三棱锥P-ABC的体积。
例2、在三棱锥P-ABC中,AB=AC=2a,∠PAB=∠PAC=∠BAC=60°,求三棱锥P-ABC的体积。
