如 何 在 立体几何解答题上得高分 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36025次 |
||
| s/upphoto/201206/20120604105501609.gif" width=48>中,
使平面 (1)求证: (2)求三棱锥 解析 、(1)在
又 (2)由(I)知 在
又
而 综上,三棱锥 【点评】解决此类问题的关键是分清折展前后哪些位置关系变了和哪些数量关系变了。 7、函数法 【命题走向】以立体几何与不等式、函数和方程、导数、平面几何等交汇处知识点为依据,考查立体几何的最值问题和极限位置问题。
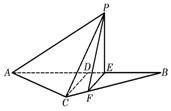
例8、如图所示,等腰三角形△ABC的底边AB= (1)求 (3)当 解析、(1)由折起的过程可知,PE⊥平面
所以四边形
即 (2)
(3)过点 于是 从而 在 故异面直线 【点评】处理立体几何解答题中的最值问题和极限位置问题,选定自变量后,就可以转化为函数问题求解了。 此文发表在《高中生·高考指导》2010年11月下旬刊 |
||
- 上一篇:构造数学模型 巧解三角问题
- 下一篇:立体几何中轨迹问题的解法
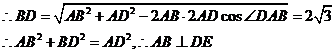
 【解法优势】利用转化思想,转化为熟知的函数知识求解。
【解法优势】利用转化思想,转化为熟知的函数知识求解。
