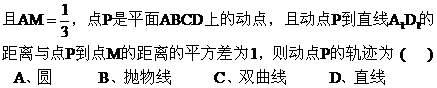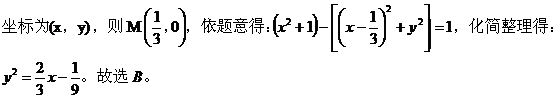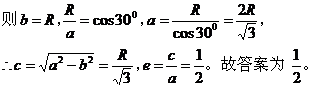立体几何中轨迹问题的解法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36863次 |
||
于真灵 立体几何中的轨迹问题,将立体几何与解析几何有机地结合起来,常涉及函数、数形结合、建模、化归等数学思想与方法,综合性强,能力要求高,近年来高考中常见的题型有:
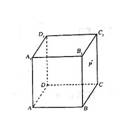
例1、如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P 到 直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( ) A、直线 B、圆 C、双曲线 D、抛物线 【解析】在侧面
的面积为定值,则动点P的轨迹是 ( ) A、圆 B、椭圆 C、一条直线 D、两条平行直线 【解析】只须保证P点到AB所在直线的距离为定值,即P的轨迹为 一个平面斜截成一个圆柱形成的截面曲线。故选B。
二、利用圆锥曲线的离心率求轨迹。 例3.已知点 一个动点,且点
的一部分,则该曲线一定是 ( ) A.圆或椭圆 B.椭圆或双曲线 C.双曲线或抛物线 D. 抛物线或圆 【解析】
例4.正方体 的中点,P是 正方体的截面,若截面为四边形,则点
【解析】由E、D、P三点确定的平面与平面 得,当P与C重合时,截面过 时点P轨迹为线段CF;而当截面过 【点评】截面图形确定后,动点的轨迹也是确定的,此时可采取执果索因的方法,确定动点所在的位置。 四、建立函数模型求函数解析式。 例5 、如图,动点 SHAPE \* MERGEFORMAT 【解析】
【点评】动点在运动过程中,当确定一个量为自变量时,轨迹问题可转化为函数问题,通过建立函数模型求出函数解析式。
例6.如图,正方体
【解析】
【点评】动点在运动过程中,有明显的等量与数量关系,可通过建立坐标系求出动点运动的轨迹方程。 六、已知截面图形,求截面所表示曲线的几何量。
【解析】如图,设椭圆的长半轴为
【点评】平面截立体几何图可得圆锥曲线,根据已知的数据可求出圆锥曲线相关的几何量。 此文发表在《湖南教育·数学教师平台》2008年11月下旬刊 |
||
- 上一篇:如 何 在 立体几何解答题上得高分
- 下一篇:高考立体几何试题的向量解法
 一、利用圆锥曲线定义求轨迹。
一、利用圆锥曲线定义求轨迹。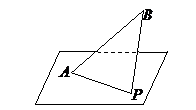 例2、如图,AB是平面
例2、如图,AB是平面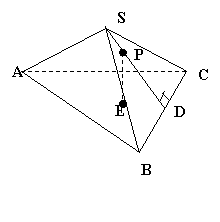 【点评】点在平面内运动的轨迹有直线、圆和圆锥曲线,直线与圆可由图形与定义直接得到,而圆锥曲线的判定方法较多,其中圆锥曲线的统一定义和圆锥曲线可由平面截立体几何图形得到是常用的方法,例1是由抛物线的定义得到,例2 是由平面斜截成一个圆柱形成的截面曲线为椭圆的方法得到。
【点评】点在平面内运动的轨迹有直线、圆和圆锥曲线,直线与圆可由图形与定义直接得到,而圆锥曲线的判定方法较多,其中圆锥曲线的统一定义和圆锥曲线可由平面截立体几何图形得到是常用的方法,例1是由抛物线的定义得到,例2 是由平面斜截成一个圆柱形成的截面曲线为椭圆的方法得到。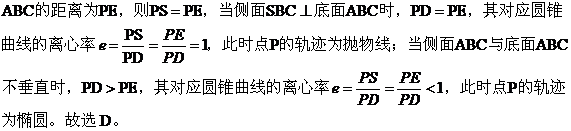 【点评】圆锥曲线的统一定义为 :到定点的距离与到定直线的距离比为常数的点的轨迹,该常数叫做圆锥曲线的离心率,用
【点评】圆锥曲线的统一定义为 :到定点的距离与到定直线的距离比为常数的点的轨迹,该常数叫做圆锥曲线的离心率,用 三、根据截面图形求轨迹。
三、根据截面图形求轨迹。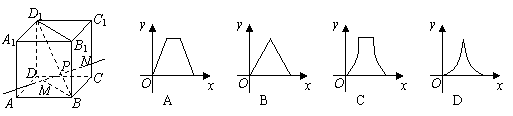
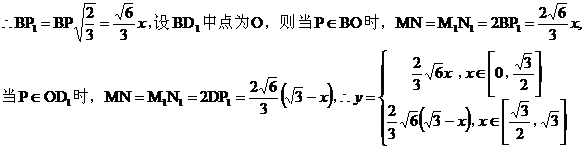 故选B.
故选B. 五、建立坐标系求轨迹方程。
五、建立坐标系求轨迹方程。