巧用对偶式解题 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:38670次 |
||
于真灵 许多数学题中的已知条件与结论之间有着相似的形式或结构,但求解却很困难,然而巧妙地构造形式相似并具有某种对称关系的一对对偶式,通过合理的运算和转化,问题便可迎刃而解. 一、轮换对偶 轮换对偶是针对式子的结构,通过轮换字母来构造对偶式. 例1. 若 求证: 证明:设
结合已知条件得: 同理: 二、倒数对偶 倒数对偶是针对式子的结构,通过对式中的某些元素取倒数来构造对偶式. 例2.设 证明:设 又 即 三、定值对偶 定值对偶是指通过运算与转换构造出定值对偶式. 例2. 设
解:构造定值对偶式:
四、共轭对偶 共轭对偶是指利用共轭根式或共轭复数来构造对偶式. 例4.已知 构造对偶复数:
五、类比对偶 类比对偶是根据已知的结论,通过类比对偶联想,得出一种新的结论,这是合情推理的猜想. 例5.求证: 证明:左边 这是角度成等比数列的3个余弦值的乘积,类比对偶:求 (1) (3) ┈┈ (5) 此文发表在《湖南教育》2011年4月下旬刊 |
||
- 上一篇:突破“概率与统计”的解题瓶颈
- 下一篇:数学难题的破解之道
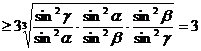 ,
,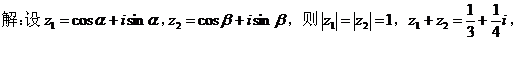
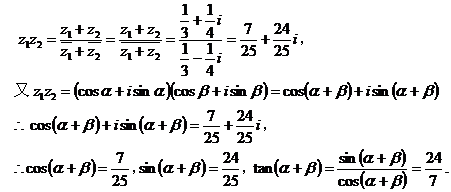
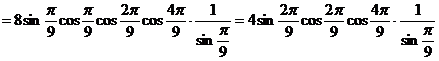
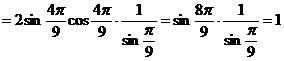 .
.
