突破“概率与统计”的解题瓶颈 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:37364次 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
于真灵 概率与统计在高中数学中是一个相对独立的内容,高考注重考查这部分内容的基本思想方法和应用,近年己逐步过渡到考查背景新颖、以学科内多个知识点综合设计或其他知识交汇融合上面来. 一、单纯的概率题 例1、某人向一目标射击4次,每次击中目标的概率为 (1)设X表示目标被击中的次数,求X的分布列; (2)若目标被击中2次, 【寻找突破口】(1)随机变量X的取值依次为0、1、2、3、4,而每次击中的结果只有“击中目标”和“未击中目标”两种可能,因此随机变量X服从二项分布,其概率可由二项分布的概率公式求得; (2)先寻求事件 则 解:(1)依题意知 则 所以
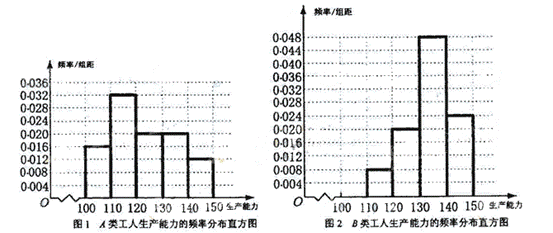
(2)设 依题意知P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3, 所求的概率为 = 【解后反思】求随机变量的分布列,要确定随机变量的取值和每个取值所对应的概率,着重分析随机变量是否服从二项分布;求概率先要分清求概率的类型:古典概型、几何概型、互斥事件和独立事件的概率、条件概率,并能熟练运用概率公式. 二、单纯的统计题 例2、某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数). (1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人; (2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2. 表1:
表2:
(i)确定 (ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表). 【寻找突破口】(1)分层抽样是等概率抽样,因此甲、乙被抽到的概率均为 (2)(i)由分层抽样可得出A类工人中应抽查25名,B类工人中应抽查75名,从而可求出 解:(1)甲、乙被抽到的概率均为 (2)(i)由题意知A类工人中应抽查25名,B类工人中应抽查75名. 故 频率分布直方图如下:
从直方图可以判断:B类工人中个体间的关异程度更小 . (ii) A类工人生产能力的平均数、B类工人生产能力的平均数以及全工厂工人生产能力的平均数的估计值分别为123、133.8和131.1 . 【解后反思】(1)简单随机抽样、分层抽样、系统抽样都是等概率抽样;(2) 画频率分布直方图要根据题目给出的条件确定区间,并求出各区间的频率. 三、概率与统计的综合题 例3、为了对某课题进行研究,用分层抽样方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
(1)求x,y; (2)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率. 【寻找突破口】(1) 分层抽样是等概率抽样,在每一层中每个个体被抽到的概率都相等;(2)这是一个古典概型,用列举法罗列出事件“这二人都来自高校C”所包含的基本事件个数和总的基本事件个数. 解:(1)由题意得: (2)记从高校B抽取的2人为 【解后反思】(1) 正确理解简单随机抽样、分层抽样、系统抽样,充分利用它们都是等概率抽样;(2)根据题意弄清所求概率类型,熟练古型概型和几何概型的定义与计算公式. 四、新情境下概率与统计的综合题
已知小球从每个叉口落入左右两个管道的可能性是相等的. 某商家按上述投球方式进行促销活动,若投入的小球落到A、B、C, 则分别设为l、2、3等奖. (1)已知获得l、2、3等奖的折扣率分别为50%、70%、90%. 记随机变量 (2)若有3人次(投l球为l人次)参加促销活动,记随机变量 【寻找突破口】(1)从题意中提取数学模型,随机变量 解:(1)
则Εξ= (2)由(1)可知,获得1等奖或2等奖的概率为 由题意得η~ 则 【解后反思】以生产、生活、科技等为背景的新情景下概率与统计综合题,应从新情景中建立起数学模式,回归到概率与统计中来,应用概率与统计的相关知识求解. 此文发表在《高中生·高考指导》2011年4月下旬刊 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- 上一篇:例谈数学阅读理解能力的培养
- 下一篇:巧用对偶式解题
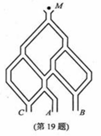 例4、如图,一个小球从M处投入,通过管道自上而下落到A或B或C.
例4、如图,一个小球从M处投入,通过管道自上而下落到A或B或C.
