高考立体几何试题的向量解法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36639次 |
||||||||||
于真灵 向量作为一种数学工具,用来处理立体几何问题,能充分体现 “数”与“形”的有机结合,淡化传统立体几何教材中的“形”到“形”的推理方法,从而降低思维难度,使解题变得程序化。下面谈一谈用向量解立体几何题的几种类型。 一、用向量处理平行问题 空间图形的平行关系包括线线平行、线面平行、面面平行,都可以用以下向量方法来处理: ①、设 ②、直线与平面平行可以转化为直线的方向向量与平面的法向量垂直。 ③、平面与平面平行可转化为两个平面的法向量平行。 ④、 例1、如图,已知四边形ABCD和ABEF为两个正方形,M、N分别在其对角线BF和AC上,且FM=AN,求证:MN∥平面EBC。
则存在实数
二、用向量处理垂直问题 空间的线线、线面、面面的垂直关系,都可以转化为空间 两个向量的垂直问题来解决。 例2、如图,已知平行六面体 的底面 ⑴、求证: ⑵、当 (1)证明:设 两两所成夹角为
从面 ⑵、解:要使
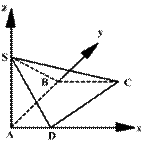
当 所以当 三、用向量处理角的问题 立体几何中所涉及的两异面直线所成的角、直线与平面所成的角、二面角等角的计算,均可化归为两个向量的夹角进行计算。
解:以AD、AB、AS为x轴、y轴、z轴,以AB为单位, 建立直角体系,则点各坐标为:
SCD的法向量为 得 所以 四、用向量处理距离问题 立体几何中所涉及的两点间的距离、点到线的距离、点和线与平面的距离均可转化为向量的模或向量 例4、在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,M、N为DC、BB1的中点,求:异面直线MN与A1B的距离。
坐标系,则点M(3,2,0),点N(0,4,1),
令y=1则z=2, 长度为: 此即异面直线MN与A1B的距离。 此文发表在《数理化学习》 2007年第3期刊 |
||||||||||
- 上一篇:立体几何中轨迹问题的解法
- 下一篇:含非特殊角及未知角三角式求值的解法
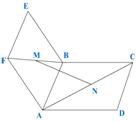
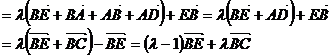
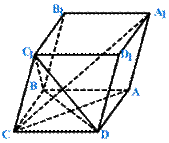
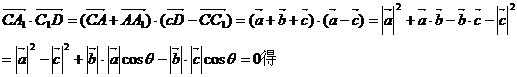
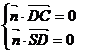 即
即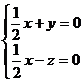 令x=1,则
令x=1,则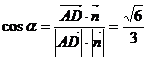 ,因此,
,因此,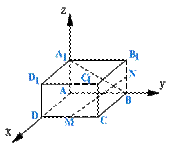
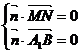 即
即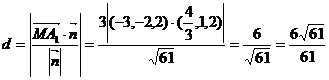 ,
,
