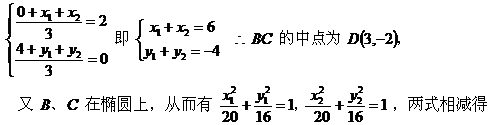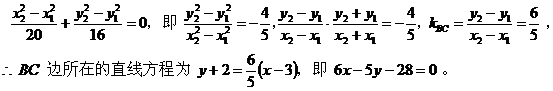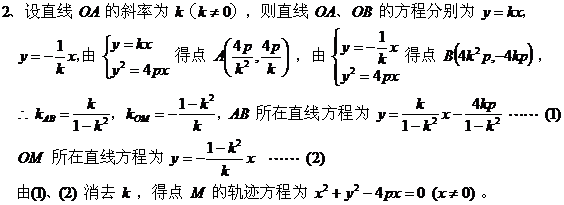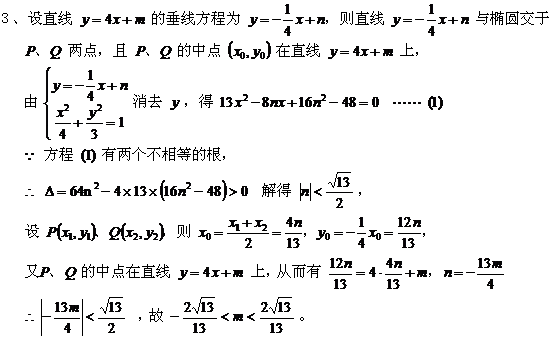设而不求--解决解析几何的金钥匙 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:35854次 |
||
“设而不求”是高中数学的一种重要思想方法,是联系解析几何与函数、方程、不等式等相关内容的纽带和桥梁,高考中许多解析几何题都能用“设而不求”解决,因此它是解决解析几何的金钥匙。如何使用这种方法,在使用过程中又应该注意哪些问题,本文举例说明。 一、哪些问题适合“设而不求” 一般说来,解题中涉及到但又不需要具体求出的中间量(称为相关量)可采用“设而不求”。 1、巧设相关点 [例1](2008年高考辽宁卷文科)在平面直角坐标系 (Ⅰ)写出C的方程; (Ⅱ)设直线 解:(Ⅰ),易求得曲线C的方程为 (Ⅱ)设
故
于是 所以 当
而 所以 [点评] 本题巧设A、B两点的坐标,但并不求出其坐标,而是利用了根与系数的关系,代入向量垂直与弦长公式直接求出K值和AB的长。高考往往在此设计题,这是最常用的解法。 2、巧设相关参数 [例2](2008年高考安徽卷文科)设椭圆 (Ⅰ)求椭圆 (Ⅱ)已知过点 (Ⅲ)过点 的最小值 解 :(I)易得:椭圆 (II)当 将其代入方程 设
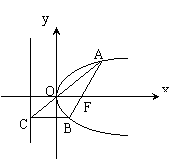
当 (III)设直线 当 [点评] 本题第(II)问巧设直线斜率K,但并不求出K,而是利用了弦长公式计算,第(III)问题巧设直线倾斜角 3、巧设相关方程 [例3](2001年高考题)
[点评] 本题巧设过F的直线方程为 K是否存在进行分类讨论。 二、“设而不求”中应注意的两个问题 1、注意隐含条件 [例4]
[点评] 方程(1)有两个不等的实根得到条件(3)是隐含条件,易被忽视,应特别当心! 2、注意参数取值范围的影响 [例5]
[点评] 消参过程中,应重视参数取值范围对其它相关变量的影响,确保等价性。 【跟踪训练】
1、椭圆的右焦点为
此文发表在《湖南教育》2009年4月下旬刊 |
||
- 上一篇:新课标高考以平面几何为依托的四类解析几何题赏析
- 下一篇:三角形形状的判断与证明
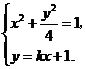 消去y并整理得
消去y并整理得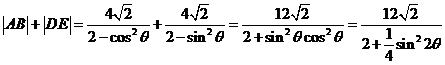
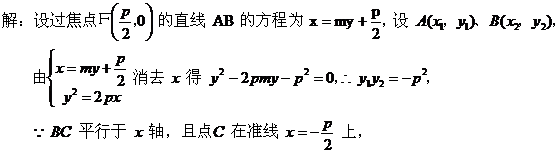
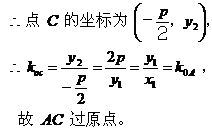
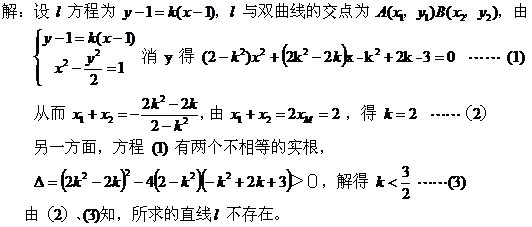
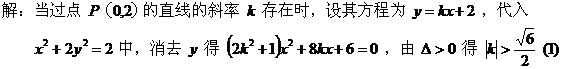
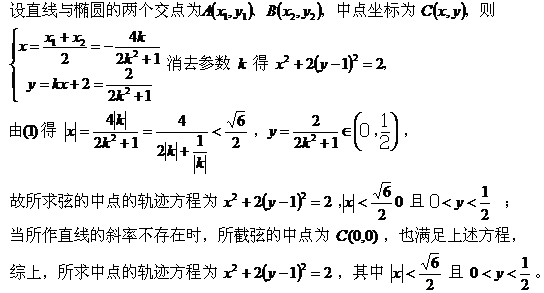

 【参考答案】
【参考答案】