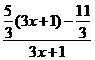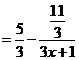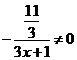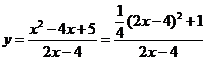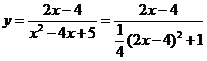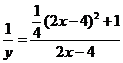例谈函数值域(最值)的求解 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-5-25 阅读:34189次 |
||||||||||||||
湖南省绥宁县第一中 吴树恒 摘要 介绍几种求函数值域的方法 关键词 函数值域,配方法,分离常数法,逆求法,均值不等式法,判别式法,单调性法,换元法,导数法 对函数三要素——解析式、定义域、值域的求解,是函数问题中出现频率比较高的问题,其中,函数值域的求解以其方法的灵活性大,题型的丰富多样而倍受出题人的青睐,也成为广大学子的大困惑,为了解决值域的求解问题,本文特通过大量实例,介绍求解值域的几种常见的方法,希望对读者有些帮助. 1、配方法 配方法通常应用在跟二次函数值域的求解有关的问题中。 例1 求函数 解:
评:对于二次函数的值域的求解,十之八九要配方,所以配方法在这里最受重用。同时,二次函数的值域的求解,通常还会借助图像,所以也可以把这种方法叫做数形结合法. 变式 (1)求 (2)求 解:(1)
且
(2)
且
评:变式中所列两例虽也进行了配方,但由于题中对 函数 (1)当
(2)当
2、分离常数法 例2 求 解:函数的定义域为
评:从上题的解答过程中,大家可以看到,通过变形后分离出了常数 3、逆求法 例3 求 分析:此例与上例的不同之处在于,多了自变量的要求,由于多了这个要求,现在我们就算分离出了常数,也不能因为 解:由
解得: 评:此题与例2的解析式虽然一样,但多了 4、均值不等式法 例4 求 解:
当且仅当
评:在此题的求解过程中,我们使用了均值不等式,所以我们把这种方法叫做均值不等式法,形如: 变式 求 解:由题知,函数的定义域为
又
当且仅当
5、判别式法 例5 求 解:令
由
当
满足要求 当
解得: 又 综上可知函数的值域为: 评:在求解过程中我们用到了判别式,所以这种方法叫做判别式法。它适用于形如 6、单调性法 例6 求 解:由题知函数的定义域为
易知,函数在 所以 所以函数的值域为 评:部分读者看到此题可能会想到用例4的均值不等式的方法去解,但是在仔细观察后可以看到在 7、换元法 例7 求 分析:要解决此题,麻烦就在于如何处理根号,为了去根号,我们决定用换元法. 解:由题知: 令
又
评:在此我们用到了换元法,这种方法一般用在含根号的问题中,换元后可以起到去根号的作用.不过不同的结构换元方法又稍有不同,比如下面一例,虽然也是换元,但换元的方法却不一样,读者要细细体味此中异同. 例8 求 解:由 设
又
评:此题一看到根号,我们马上就想到了换元,但是用例7的方法换元后,发现还是去不了根号,甚至得到的式子比原来更复杂了,所以只能想别的方法,又考虑到自变量的取值范围和被开方式的结构都跟三角函数的结构特征相关,所以我们采用了三角换元,大家注意他们二者之间的差异. 8、导数法 例9 求 解: 令 则:
所以函数的最小值是 所以函数的值域为 评:用导数可以求很多形式函数的值域,通常来讲的话,那些求了导以后式子变简单了,好求解了的函数,可以用导数法去试试. 总之,求函数的值域是高中数学中的难度比较大的问题,题型丰富,方法灵活,大家细细体味本文中的几种方法后在学习过程中融会贯通.希望本文能对大家有些帮助。 (此文在2011年参评湖南省教育协会论文大赛获叁等奖) |
||||||||||||||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667