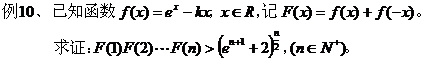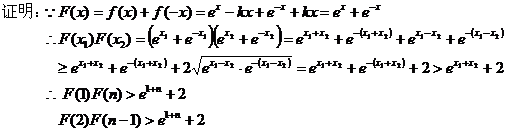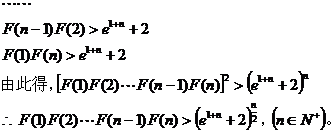函数背景下不等关系的判定与证明 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:33220次 |
||
于真灵 函数问题历来是高考命题的重点,考查内容全面,设计新颖,形式多样,综合性强,其中以函数为背景的不等式问题,是知识网络的一个交汇点,同时也是高考数学命题的热点之一。探求函数背景下的不等问题,实质是将函数的有关性质进行适当转化,再归纳为某个不等式问题,其中函数的定义、解析式、性质、图像特征,是问题转化的知识基础。因此,在实际解题中要注重从概念、解析式、性质、图像出发,进行逻辑分析、推理和判断,并结合不等式的相关知识进行求解。下面例析高考中常见的题型。 一、利用函数的解析式求值: 例1、若函数 A、 C、
数值的大小。 二、利用函数的周期性: 例2、已知 A、 解析:已知 设 ∴ 点评:利用函数的周期性可将自变量对应的函数值转化到同一区间内所对应的函数解析式下求值或同一单调区间内比较函数值的大小。 三、利用函数图像的对称性:
点评:利用函数图像的对称性可将自变量对应的函数值转化到同一区间内所对应的函数解析式下求值或同一单调区间内比较函数值的大小。 四、根据函数图像特征:
是( ) A、 C、
点评:根据函数图像的特性并结合函数性质,可得出相关量间的不等关系。 五、结合导数,利用函数的单调性:
点评:结合导数,利用函数的单调性可解出所含变量的取值范围或得出相关量间的不等关系。 六、化归思想:
点评:根据题设条件将比较大小的量化归为同一种函数所对应的函数值,再根据这种函数的单调性进行大小比较。 七、数形结合思想:
点评:根据题设条件做出函数的图像,根据函数 图像特征化归为几何图像求解。 八、给出某些特性,判断函数具备这些特性: 例8、在下列四个函数中,满足性质: “对于区间 A、 解析:
点评:这类题通常采用验证法,利用函数本身的性质,再运用放缩等方法验证选项中所给的函数具备这些特性。 九、构造函数:
点评:本题应用了放缩法和累乘法。 函数背景不等关系判断与证明的方法很多,但熟练地掌握了以上各种方法,再用一些常用的数学思想,辅助以适当的解题技巧,加上一定的综合解决问题的能力,便能迎刃而解。 此文发表在《理科考试研究》期刊2010年8月刊 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

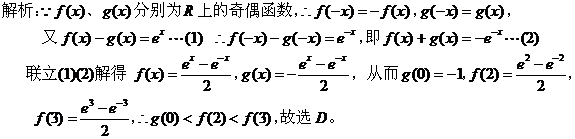 点评:根据题设条件直接求出函数解析式,再求出所对应的函数值,然后比较函
点评:根据题设条件直接求出函数解析式,再求出所对应的函数值,然后比较函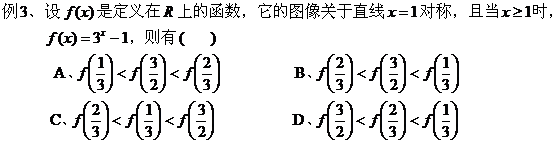
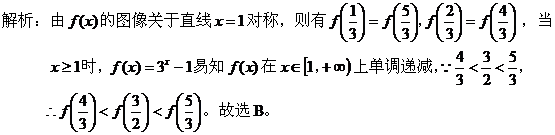
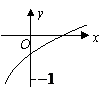 例4、已知函数
例4、已知函数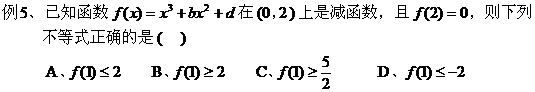
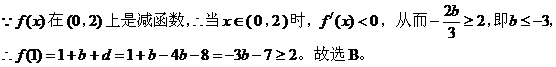
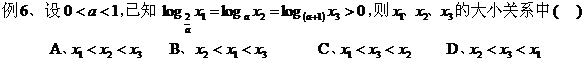
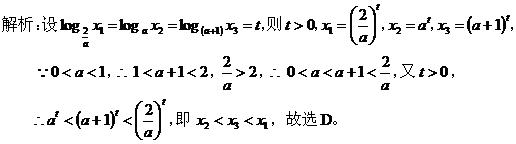
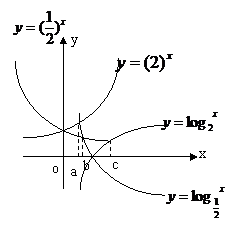
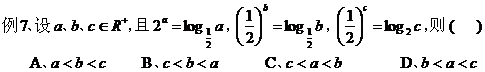

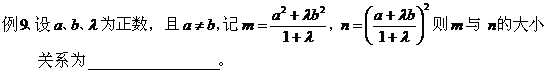
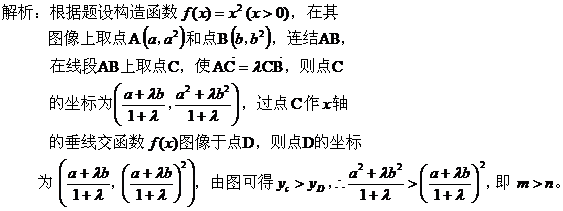
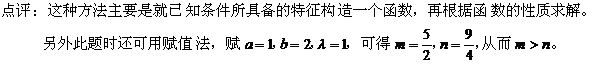 十、证明不等关系:
十、证明不等关系: