高考中常见的几类创新题的求法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:35561次 |
||
于真灵 近年来,《考试大纲》中明确提出了创新意识和实践能力的考查要求,全国各地高考中出现了具有新颖的信息与情境的“创新题”,对此进行归纳,以加强高三复习的针对性。
例1:(06年上海(文)12题) 如图,平面中两条直线 相交于点 直线 “距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是 4 。 例2:(07年福建(理)16题)中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合 (1)自反性:对于任意 (2)对称性:对于 (3)传递性:对于 则称“ 答案:不唯一,如“图形的全等”、“图形的相似”、“非零向量的共线”、“命题的充要条件”等等. 点评:以新概念、新定义给出创新题是全国各地高考中常见的一种形式,解决这类题的关键是准确理解题目中的新概念、新定义,然后用“老知识”加以解决。 二、以新运算给出发散型创新题。 例3:(07年广东(理)8题)设 A. C. 答案:不妨设
点评:解决这类题的关键是准确把握好新运算的规则、公式、数据处理模式,能根据问题的条件,寻找与新运算相符的运算途径,做出运算、判断、推理。 三、以新的知识载体给出背景新颖的创新题
同一路段上驶入与驶出的车辆数相等),则 (A) (C) 解:依题意,有x1=50+x3-55=x3-5,\x1 例5:(06年陕西(理)12题)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为 A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7 解析:当接收方收到密文14,9,23,28时, 则
环形分布图,公司在年初分配给 A、 B、C、D 四个维修点某种配 件各50件.在使用前发现需将 A、B、C、D 四个维修点的这批 配件分别调整为40、45、54、61件,但调整只能在相邻维修 点之间进行.那么要完成上述调整,最少的调动件次( 件从一个维修点调整到相邻维修点的调动件次为 A、18 B、17 C、16 D、15
点评:以新的知识载体给出的创新题的显著特征是与其它知识的组合与融汇,这类题考查的目标是实践能力,要求综合应用所学数学知识、思想和方法理解陈述的材料,并能用数学语言正确地表达和说明。 四、以新的知识交汇点给出的创新题,抓住主要矛盾探索解决问题的思路 例7:(06年上海(理)10题) 如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 (A)48 (B) 18 (C) 24 (D)36 解:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”,选D.。 例8:(07年湖南理10题)设集合 A.10 B.11 C.12 D.13
此文发表在《数理化学习》2008年10月刊 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

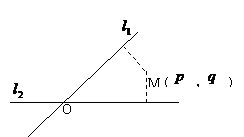 一、以新概念、新定义给出信息迁移型创新题
一、以新概念、新定义给出信息迁移型创新题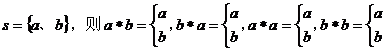
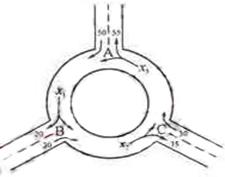 例4:(06年北京(理)8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口
例4:(06年北京(理)8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口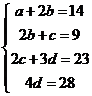 ,解得
,解得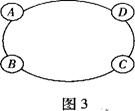 例6、(07年广东(理)7 题)图3是某汽车维修公司的维修点
例6、(07年广东(理)7 题)图3是某汽车维修公司的维修点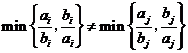 (
(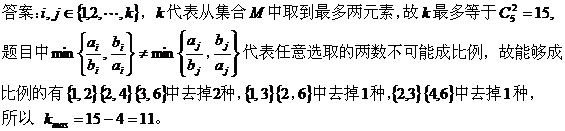 点评:解决这类问题时一定要透过现象看本质,认清题目所属的真正类型。
点评:解决这类问题时一定要透过现象看本质,认清题目所属的真正类型。






