高考中常见线性规划题的解法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:35833次 |
||
于真灵 线性规划是高中数学新增内容之一,也是近年来高考一个新的亮点与热点问题,随着新教材的逐步推进,线性规划正逐渐成为中学数学知识的一个重要交汇点,它正悄悄地与函数、不等式、解几、立几、导数等建立多种联系,相互渗透,使问题的情景新颖而别致。下面介绍几类高考中常见线性规划题的解法。 一、求满足可行域的不等式(组):
点评:此类题先确定边界的直线(曲线)方程, 再用特殊点确定所求的区域。 二、求目标函数的最值:
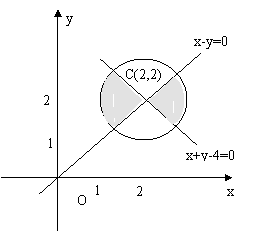
三、求可行域表示区域的面积:
点评:先确定可行域,再根据可行域表示的图形利用平面几何图形求面积。 四、利用距离公式求最值:
五、利用斜率公式求范围:
六、根据条件确定可行域:
此文发表在《语数外学习 |
||
推荐使用Chorme或国内浏览器的“极(快)速模式”浏览 【后台管理】 主办单位:绥宁县第一中学
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

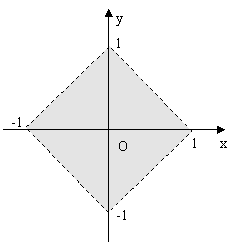 例1、如右图,平面区域内(不含边界的阴影部分) 的点用不等式表示为 ( B )
例1、如右图,平面区域内(不含边界的阴影部分) 的点用不等式表示为 ( B )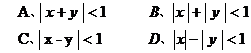

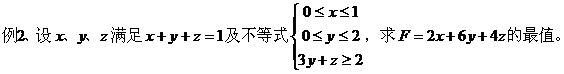
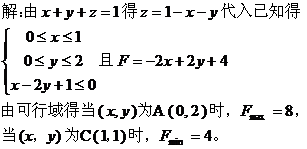

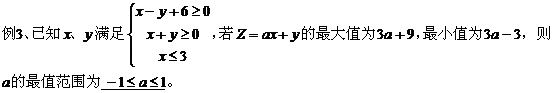
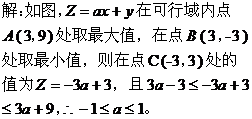

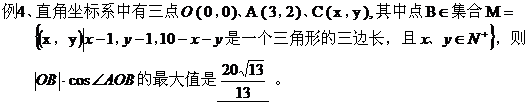
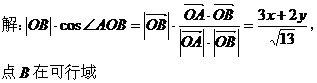
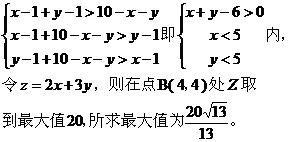
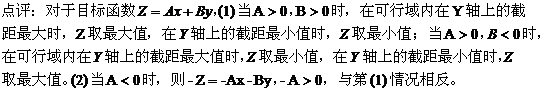
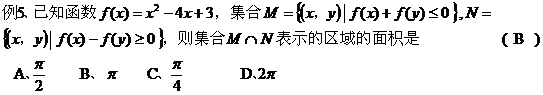
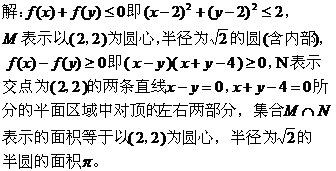

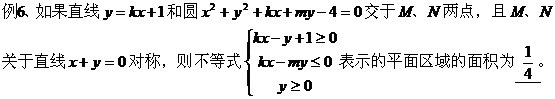
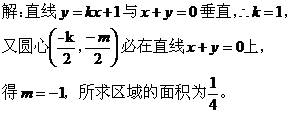

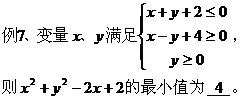
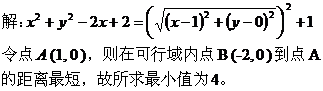

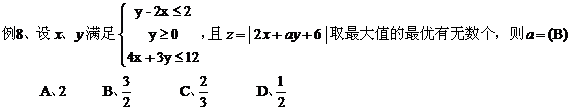
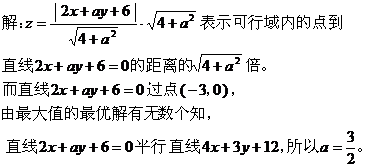
 点评:将所求的最值化为两点间、点到直线的距离,再在可行域内求一点到已知点或直线的距离的最大(小)值。
点评:将所求的最值化为两点间、点到直线的距离,再在可行域内求一点到已知点或直线的距离的最大(小)值。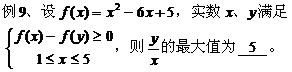
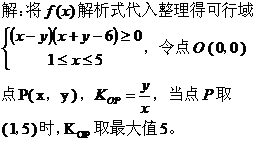
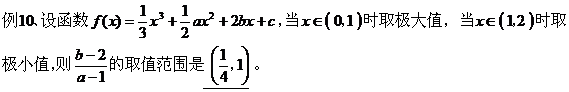
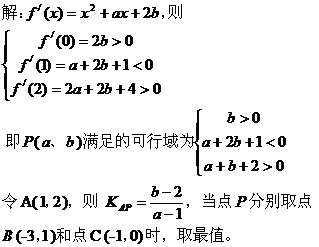
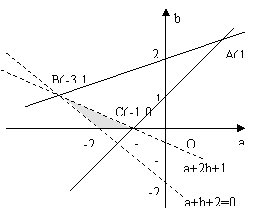 评:先确定可行域,将所求式子转变为已知两点求直线斜率公式,再在可行域内求一点到已知点的斜率的最值。
评:先确定可行域,将所求式子转变为已知两点求直线斜率公式,再在可行域内求一点到已知点的斜率的最值。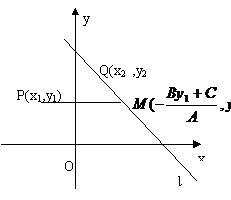
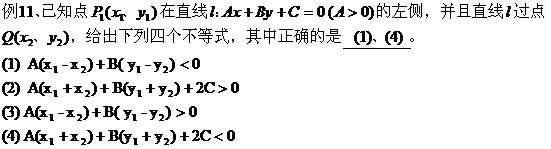
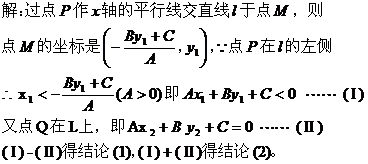
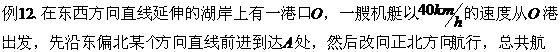


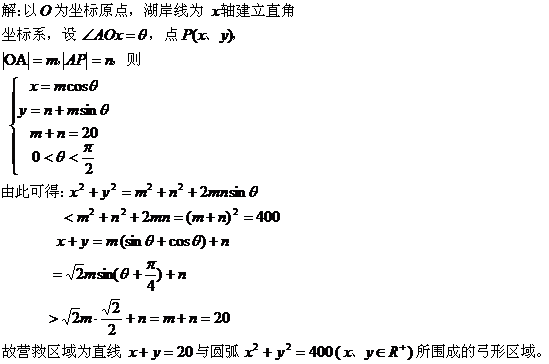 以上各例说明解决这类问题,需要我们熟练地掌握以上各种类型,用化归思想、数形结合思想等一些常用的数学思想和数学方法,辅助以适当的解题技巧,再加上一定的综合解决问题的能力,便能迎刃而解。
以上各例说明解决这类问题,需要我们熟练地掌握以上各种类型,用化归思想、数形结合思想等一些常用的数学思想和数学方法,辅助以适当的解题技巧,再加上一定的综合解决问题的能力,便能迎刃而解。






