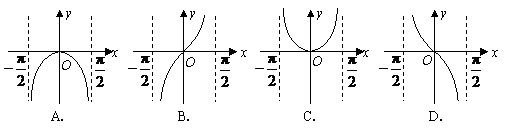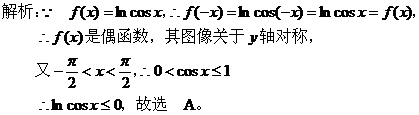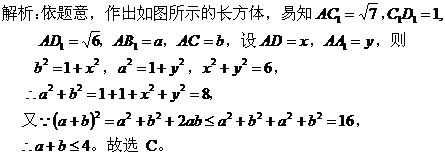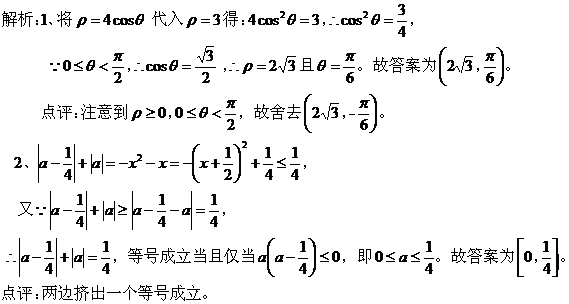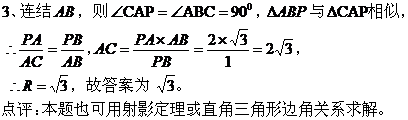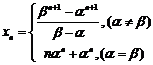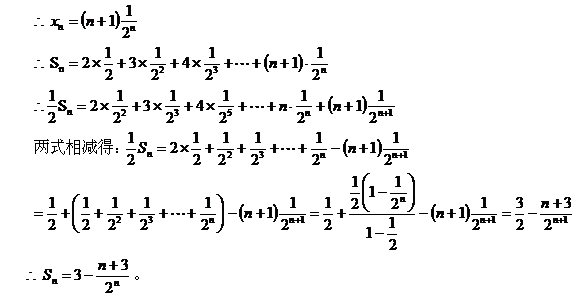新课程高考数学呈现的主要特征 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36571次 |
||
于真灵 高中新课程已全面铺开,新课程在继承与发扬传统课程理念的基础上,适应时代的发展,注入了新的标准和新的理念,这必将给高考带来新一轮的革命。综观江苏、山东、海南、宁夏、广东等高中新课程实验省市的近几年高考,新课程高考数学呈现出以下主要特征。 一、注重“双基”的考查。 数学新课程标准中,将数学教学定位为重视基础知识教学、基本技能训练和能力培养,在以“学生为本”的前提下,强调教学中应删减繁琐的计算、人为技巧化的难题和过分强调细枝 末节的内容,克服“双基异化”的倾向。因此“双基”仍是教学与考试的重点。 【例1】(08年江苏卷)
二、强化通性通法的考查。 数学新课程标准中,仍强调数学知识的通性和解数学题的通法,因此通性通法仍是教学与考试的重点。 【例2】(08年山东卷)函数 SHAPE \* MERGEFORMAT
【点评】判断函数图像的通常方法是先确定定义域、值域,再确定奇偶性与单调性,根据这些性质便可确定函数的大致图像。 三、加强对新增知识的考查。 数学新课程必修教材中新增了算法、二分法、三视图、古典概型、几何概型等内容,新增内容往往是高考出题的热点,而且会常考常新。 【例3】(08年海南卷)某几何体的一条棱长为 A、
【点评】这是一道在三视图背景下设计的立体几何题,主要考查空间想象力、几何图形的相互转化能力,以及均值不等式的应用。 四、探究对选修内容的考查。 数学新课程增加了选修教材,为学生提供多层次、多种类的选择,以满足学生自身的基本需求,促进学生的个性发展。选修教材的选取,给教学提供了一定的空间,这会成为新课程高考数学一个新的亮点。 【例4】(08年广东卷)选做题(1—3题,考生只能从中选做两题) 1、(坐标系与参数方程选做题)已知曲线 2、(不等式选讲选做题)已知 3、(几何证明选讲选做题)已知
五、重视对多向思维和创新思维的考查。 数学新课程标准中,把培养学生的自主学习、自主探究能力,作为发展学生创新思维和创新能力的重要渠道,因此,培养和考查学生多向思维与创新思维,是数学新课程的一个重要目标。 【例5】(08年广东卷)设 (1)证明: (2)求数列 (3)若 解析:(1)由求根公式,不妨设
(2)设 得, 由题意可知, ①当
即 由等比数列性质可得 两式相减,得
②当 即
即
综上所述, (3)把
【点评】(1) 该问看似简单,利用根与系数关系可直接得到,但这是设计的陷阱,其实是要求证明根与系数间的关系。它考查学生的思辨能力。 (2) 该问用到构造法、代换法、分类讨论等数学思想与方法,综合性强,考查学生的多种思维能力与创新思维能力。 (3) 数列求和的方法有公式法、裂项求和、倒序相加、错位相减等方法,能根据数列通项特征快捷准确地找到方法,它考查学生思维的敏捷性。 此文发表在《高中生·高考指导 》2008年11月下旬刊 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

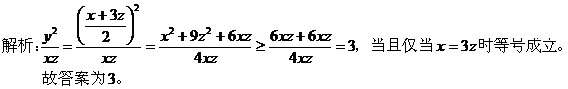 【点评】这道题考查的基础知识是均值不等式,基本技能是消元法。
【点评】这道题考查的基础知识是均值不等式,基本技能是消元法。