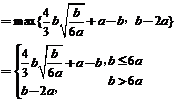∴ 在（一1，1 ）内有唯一实根。

因此，当 时， 有两个不同的根 满足 ；当  时

有三个不同的根 ，满足 。

现考虑函数 的零点：

( i ）当 时， 有两个根 ，满足 。

而 有三个不同的根， 有两个不同的根，故 有5 个零点。

( 11 ）当 时， 有三个不同的根 ，满足 。

而 有三个不同的根，故 有9 个零点。

综上所述，当 时，函数 有5 个零点；当 时，函数 有9 个零点。

【考点】函数的概念和性质，导数的应用。

【解析】（1）求出 的导数，根据1和 是函数 的两个极值点代入列方程组求解即可。

       （2）由（1）得， ，求出 ，令 ，求解讨论即可。

       （3）比较复杂，先分 和 讨论关于  的方程  根的情况；再考虑函数 的零点。

21.【2012高考真题辽宁理21】本小题满分12分)

设 ，曲线 与

直线 在(0，0)点相切。

   (Ⅰ)求 的值。

   (Ⅱ)证明：当 时， 。

【答案】

【点评】本题综合考查导数的概念、几何意义、导数在判断函数单调性与最值中的运用。本题容易忽略函数 的定义域，根据条件曲线 与直线 在(0，0)点相切，求出 的值，然后，利用函数的单调性或者均值不等式证明 即可。从近几年的高考命题趋势看，此类型题目几乎年年都有涉及，因此，在平时要加强训练。本题属于中档题。

22.【2012高考真题重庆理16】（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分.）

设 其中 ，曲线 在点 处的切线垂直于 轴.

（Ⅰ）求 的值；

（Ⅱ）求函数 的极值.

 【答案】

23.【2012高考真题浙江理22】(本小题满分14分)已知a＞0，b R，函数 ．

(Ⅰ)证明：当0≤x≤1时，

(ⅰ)函数 的最大值为|2a－b|﹢a；

(ⅱ) ＋|2a－b|﹢a≥0；

(Ⅱ) 若﹣1≤ ≤1对x [0，1]恒成立，求a＋b的取值范围．

【命题立意】本题主要考查不等式、利用导数研究函数的单调性等性质、线性规划等知识点综合运用能力，同时考查抽象概括、推理论证能力。

【答案】本题主要考察不等式，导数，单调性，

(Ⅰ)(ⅰ) ．

当b≤0时， ＞0在0≤x≤1上恒成立，

此时 的最大值为： ＝|2a－b|﹢a；

当b＞0时， 在0≤x≤1上的正负性不能判断，

此时 的最大值为：

＝|2a－b|﹢a；

综上所述：函数 在0≤x≤1上的最大值为|2a－b|﹢a；

(ⅱ) 要证 ＋|2a－b|﹢a≥0，即证 ＝﹣ ≤|2a－b|﹢a．

亦即证 在0≤x≤1上的最大值小于(或等于)|2a－b|﹢a，

∵ ，

∴令 ．

当b≤0时， ＜0在0≤x≤1上恒成立，

此时 的最大值为： ＝|2a－b|﹢a；

当b＜0时， 在0≤x≤1上的正负性不能判断，

≤|2a－b|﹢a；

综上所述：函数 在0≤x≤1上的最大值小于(或等于)|2a－b|﹢a．

即 ＋|2a－b|﹢a≥0在0≤x≤1上恒成立．

(Ⅱ)由(Ⅰ)知：函数 在0≤x≤1上的最大值为|2a－b|﹢a，

且函数 在0≤x≤1上的最小值比﹣(|2a－b|﹢a)要大．

∵﹣1≤ ≤1对x [0，1]恒成立，

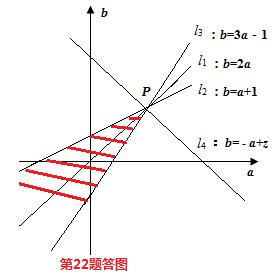
∴|2a－b|﹢a≤1．

取b为纵轴，a为横轴．

则可行域为： 和 ，目标函数为z＝a＋b．

作图如下：

由图易得：当目标函数为z＝a＋b过P(1，2)时，有 ．

∴所求a＋b的取值范围为： ．

24.【2012高考真题山东理22】(本小题满分13分)

已知函数 （ 为常数， 是自然对数的底数），曲线 在点 处的切线与 轴平行.

（Ⅰ）求 的值；

（Ⅱ）求 的单调区间；

（Ⅲ）设 ,其中 为 的导函数.证明：对任意 .

【答案】

25.【2012高考真题湖南理22】（本小题满分13分）

已知函数 = ，其中a≠0.

（1）       若对一切x∈R， ≥1恒成立，求a的取值集合.

（2）在函数 的图像上取定两点 ， ，记直线AB的斜率为K，问：是否存在x₀∈（x₁，x₂），使 成立？若存在，求 的取值范围；若不存在，请说明理由.

【答案】（Ⅰ）若 ，则对一切 ， ，这与题设矛盾，又 ，

故 .

而 令

当 时， 单调递减；当 时， 单调递增，故当 时， 取最小值

于是对一切 恒成立，当且仅当

　　　　　 .　　　　　　　　　　　　　　　　　　①

令 则

当 时， 单调递增；当 时， 单调递减.

故当 时， 取最大值 .因此，当且仅当 即 时，①式成立.

综上所述， 的取值集合为 .

（Ⅱ）由题意知，

令 则

令 ，则 .

当 时， 单调递减；当 时， 单调递增.

故当 ， 即

从而 ， 又

所以

因为函数 在区间 上的图像是连续不断的一条曲线，所以存在 使 单调递增，故这样的 是唯一的，且 .故当且仅当 时， .

综上所述，存在 使 成立.且 的取值范围为

.

【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想，转化与划归思想等数学思想方法.第一问利用导函数法求出 取最小值 对一切x∈R，f(x) 1恒成立转化为 ，从而得出a的取值集合；第二问在假设存在的情况下进行推理，通过构造函数，研究这个函数的单调性及最值来进行分析判断.

2012年高考真题汇编——理科数学：3：导数（www.ks5u.com 2012高考）.doc