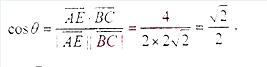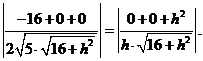2012年高考真题汇编——理科数学:7:立体几何 来源:绥宁一中校园网 作者:吴树恒 更新时间:2012-6-25 阅读:38903次 |
||
| lt=高考资源网(ks5u.com),中国最大的高考网站,您身边的高考专家。 src="http://img.snyzedu.com/images/upphoto/201206/20120619125508118.gif" width=53 height=24> 所在平面都与平面
(Ⅰ)证明: (Ⅲ)求二面角 【答案】本题考查平面图形与空间图形的转化,空间直线与直线、直线与平面、平面与平面的位置关系的判定。空间线段长度和空间角的余弦值的计算等基础知识和基本技能,考查空间想象能力,推理论证能力和求解能力。 【解析】(综合法) ( = 1 \* ROMAN I)取 则 同理: 又 (Ⅱ)延长
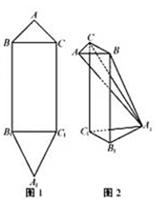
(Ⅲ) 在 在 得:二面角 37.【2012高考真题上海理19】(6+6=12分)如图,在四棱锥 底面 (1)三角形 (2)异面直线
【答案】 【解析】(1)∵PA⊥底面ABCD,∴PA⊥CD, 又∵CD⊥AD,∴CD⊥平面PAD, ∴CD⊥PD, 又∵ ∴△PCD的面积为 (2)解法一:取PB的中点F,连接EF,AF, 则EF∥BC,∴∠AEF(或其补角)是异面直线 BC与AE所成的角。 在△ADF中,EF= ∴△AEF是等腰直角三角形, ∴∠AEF= ∴异面直线BC与AE所成的角大小为 解法二:如图所示,建立空间直角坐标系, 则B(2,0,0),C(2, 设
又∵0<
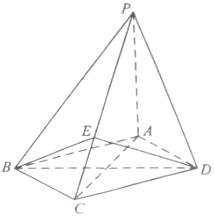
【点评】本题主要考查直线与直线、直线与平面的位置关系,考查空间想象能力和推理论证能力.综合考查空间中两条异面直线所成的角的求解,同时考查空间几何体的体积公式的运用.本题源于《必修2》立体几何章节复习题,复习时应注重课本,容易出现找错角的情况,要考虑全面,考查空间想象能力,属于中档题. 38.【2012高考真题全国卷理18】(本小题满分12分)(注意:在试题卷上作答无效) 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2
(Ⅰ)证明:PC⊥平面BED; (Ⅱ)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小. 【答案】
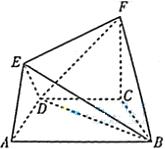
39.【2012高考真题山东理18】(18)(本小题满分12分) 在如图所示的几何体中,四边形 (Ⅰ)求证: (Ⅱ)求二面角 【答案】
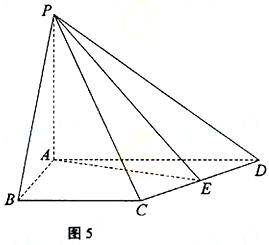
40.【2012高考真题湖南理18】(本小题满分12分) 如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点. (Ⅰ)证明:CD⊥平面PAE; (Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
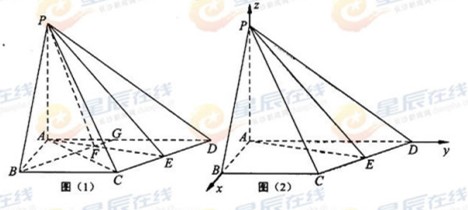
【答案】解法1(Ⅰ如图(1)),连接AC,由AB=4,
而 (Ⅱ)过点B作 由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是 所成的角,且 由
因为 由 在 于是 又梯形
解法2:如图(2),以A为坐标原点,
(Ⅰ)易知
(Ⅱ)由题设和(Ⅰ)知,
由(Ⅰ)知,
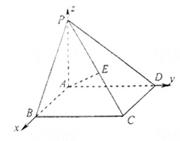
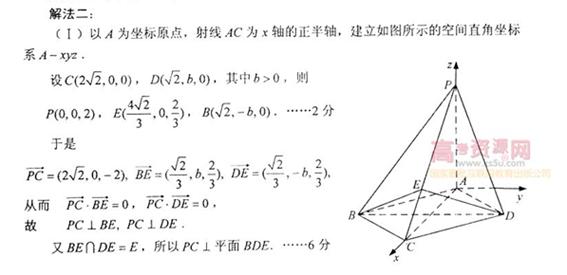
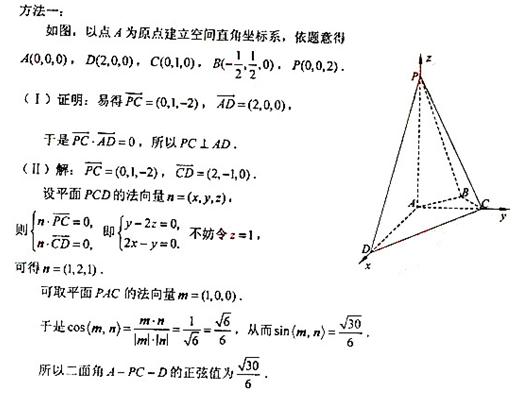
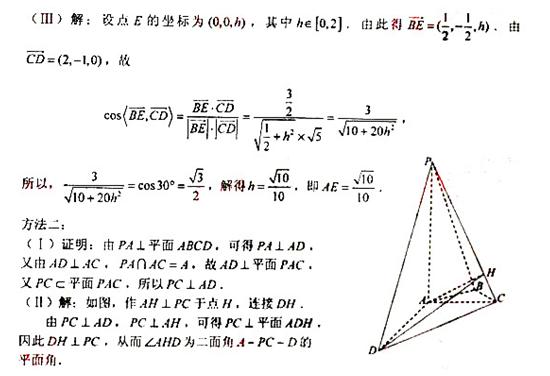
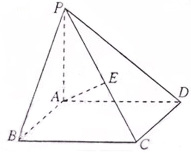
解得 又梯形ABCD的面积为 41.【2012高考真题天津理17】(本小题满分13分) 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. (Ⅰ)证明PC⊥AD; (Ⅱ)求二面角A-PC-D的正弦值; (Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
【答案】
|
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

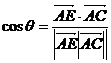 =
=