2012年高考真题——数学理(湖南卷)word版含解析 来源:绥宁一中校园网 作者:吴树恒 更新时间:2012-6-25 阅读:44095次 |
||
| t=高考资源网(ks5u.com),中国最大的高考网站,您身边的高考专家。 src="/images/upphoto/201206/20120619141106983.gif" width=65 height=19>
由 在 于是 又梯形
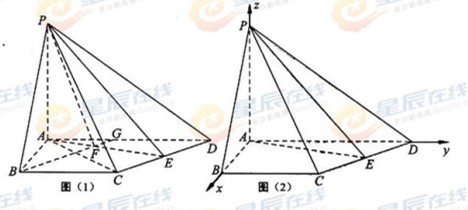
解法2:如图(2),以A为坐标原点,
(Ⅰ)易知
(Ⅱ)由题设和(Ⅰ)知,
由(Ⅰ)知,
解得 又梯形ABCD的面积为 【点评】本题考查空间线面垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明 19.(本小题满分12分) 已知数列{an}的各项均为正数,记A(n)=a1+a2+……+an,B(n)=a2+a3+……+an+1,C(n)=a3+a4+……+an+2,n=1,2,…… [来^&源:中教网@~%] (1) 若a1=1,a2=5,且对任意n∈N﹡,三个数A(n),B(n),C(n)组成等差数列,求数列{ an }的通项公式. (2) 证明:数列{ an }是公比为q的等比数列的充分必要条件是:对任意 【解析】 解(1)对任意 即 故数列 (Ⅱ)(1)必要性:若数列
即 (2)充分性:若对于任意 则 于是 由 因为 综上所述,数列 【点评】本题考查等差数列、等比数列的定义、性质及充要条件的证明.第一问由等差数列定义可得;第二问要从充分性、必要性两方面来证明,利用等比数列的定义及性质易得证. 20.(本小题满分13分)[来#源:中教%&*网~] 某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数). (1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间; (2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案. 【解析】 解:(Ⅰ)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为
期中 (Ⅱ)完成订单任务的时间为
(1)当 由函数
故当 (2)当
由函数 此时完成订单任务的最短时间大于 (3)当 当 完成订单任务的最短时间为 综上所述,当 分别为44,88,68. 【点评】本题为函数的应用题,考查分段函数、函数单调性、最值等,考查运算能力及用数学知识分析解决实际应用问题的能力.第一问建立函数模型;第二问利用单调性与最值来解决,体现分类讨论思想. 21.(本小题满分13分)[www.z%zstep.co*~&m^] 在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值. (Ⅰ)求曲线C1的方程; (Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值. 【解析】(Ⅰ)解法1 :设M的坐标为
易知圆
化简得曲线 解法2 :由题设知,曲线 (Ⅱ)当点P在直线
整理得
设过P所作的两条切线
由 设四点A,B,C,D的纵坐标分别为
同理可得
于是由②,④,⑤三式得
所以,当P在直线 【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问用直接法或定义法求出曲线的方程;第二问设出切线方程,把直线与曲线方程联立,由一元二次方程根与系数的关系得到 22.(本小题满分13分) 已知函数 (1) 若对一切x∈R, (2)在函数 【解析】(Ⅰ)若 故 而 当 于是对一切 令 当 故当 综上所述, (Ⅱ)由题意知, 令
令 当 故当 从而 所以 因为函数 综上所述,存在
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想,转化与划归思想等数学思想方法.第一问利用导函数法求出 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

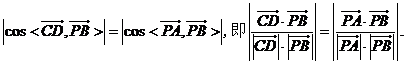
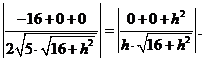
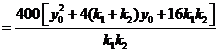
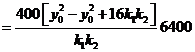 .
.







