三角函数中参数取值问题的解法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:37154次 |
||||
于真灵 三角函数中参数取值问题是高考中的重要考试内容之一,常用到函数与方程思想、不等式思想、化归思想、数形结合思想等。纵观高考试题,选择题、填空题、解答题中每年都有三角函数中参数取值的题。近年来高考中常见的题型有: 一、利用正(余)弦函数的有界性 【例1 】设 C.有最大值且有最小值 D.既无最大值又无最小值 解析:令 【点评 】函数
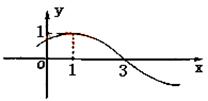
二、利用三角函数的图像 【例2 】
A. C. 【点评 】
三、利用三角函数的单调性 【例3 】已知函数y =tan (A)0 <
【点评 】
【例4 】
五、利用三角函数的奇偶性 【例5 】设函数 解析:
【例6 】若 解析:ab≠0,
【点评 】
六、利用三角函数的对称性 【例7 】
【例8 】
【点评 】
七、利用正(余)弦函数的最值 【例9 】
【点评 】 八、利用数形结合法 【例10 】
九、利用分离变量法 【例11 】已知函数 解:
又
十、利用分段函数 【例12 】已知函数 (A)1 (B)
此文发表在《考试·高考数学》2009年3-4月刊 |
||||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

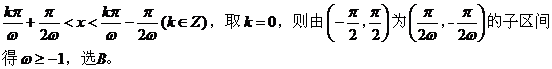 解:
解: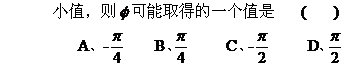
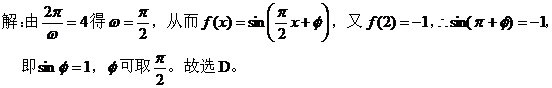 【点评 】
【点评 】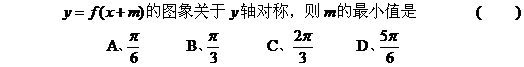
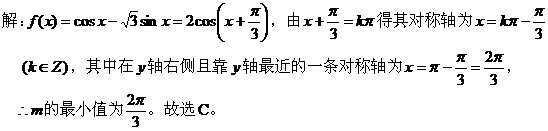
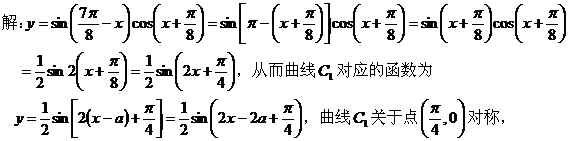
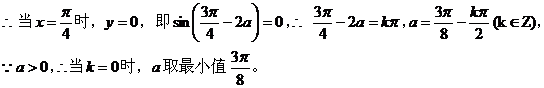

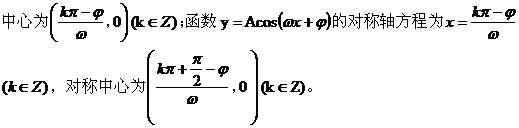
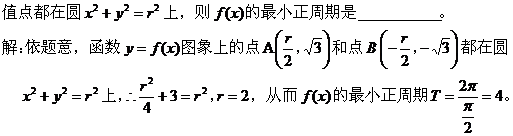
 【点评 】此题利用数形结合,将所求问题转化为图像位置关系来处理。
【点评 】此题利用数形结合,将所求问题转化为图像位置关系来处理。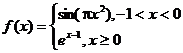 ,若
,若