新课标高考以平面几何为依托的四类解析几何题赏析 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36439次 |
||
以平面几何为依托的解析几何综合题在新课标高考中频频出现,这类综合题题意新颖、构思精巧,极富思考性和挑战性,充分体现了变知识立意为能力立意,在知识的网络交汇点设计试题的新课标高考命题的指导思想,具有较好的区分度和选拔功能。下面笔者精选四道2009年高考试题予以分类解析,旨在探索题型规律,掌握解题方法。 一、以直线为依托的解几综合题
则 (II)由(I)知椭圆的方程为 由题意知 代入椭圆的方程中整理得 由韦达定理有: .假设存在点P,使 点 整理得 又 故 将
当 当 评析:直线与圆锥曲线的位置关系,高考中常以压轴题形式出现,重点考查推理论证及运算能力,常用“设而不求法”将向量条件转化为坐标表示,再利用一元二次方程根与系数的关系解决。 二、以三角形为依托的解几综合题 例2、(09年,湖北理20题)过抛物线 (Ⅰ)当 (Ⅱ)记 解:依题意,可设直线MN的方程为
由 从而有 于是 又由 (1)
(Ⅱ)存在
将①、②、③代入上式化简可得
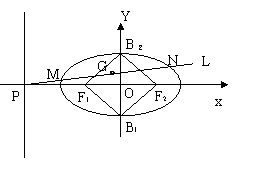
上式恒成立,即对任意 评析:本题主要考查抛物线的定义和几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力。有关三角形与圆锥曲线的结合,要注重三角形相关性质及面积公式的运用。 三、以四边形为依托的解几综合题 例3、(09年,湖南文20题) 已知椭圆C的中心在原点,焦点在 (1)求椭圆C的方程:w.w.w.k.s.5.u.c.o.m (2)设点P是椭圆C的左准线与 解: (1) 依题意,设椭圆C的方程为 (2)椭圆C的左准线方程为
线段MN的中点为G
由 因为 因为 别为
解得 故直线 评析:本题主要考查椭圆的几何性质,第(2)问关键在于寻找线段MN中点在正方形内的充要条件,转化为直线与椭圆的位置关系,应用一元二次方程根与系数的关系来求解。 四、以圆形为依托的解几综合题 例4、(09年,江西文22题)如图,已知圆 的内接△
(2)过点 证明:直线 解: (1)设
即 而点 由(1)、 (2)式得 (2) 设过点 则 解得 将(3)代入 设 则直线 于是直线 即 评析:本题主要考查利用解析几何知识求解与圆有关综合问题的能力。圆切线性质的应用与圆切线的证明是解决本题的关键。证明直线与圆相切既可用几何法也可用代数法。 此文发表在《考试·高考数学》2010年7-8月刊 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

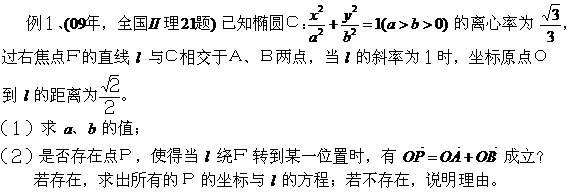
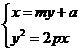 消去x可得
消去x可得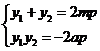 ①
①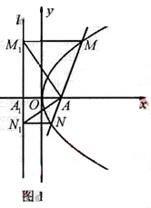 记直线
记直线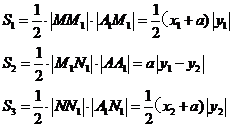 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 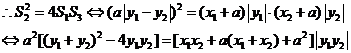
 如图,设点M、N的坐标分别为
如图,设点M、N的坐标分别为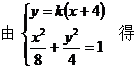
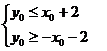 即
即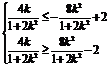 亦即
亦即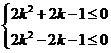 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 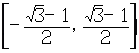 。
。 (1)求圆
(1)求圆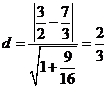 ,故结论成立。
,故结论成立。






