递推数列中不等式问题的解法 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:37227次 |
||
递推数列中的不等式问题,在选择题、填空题和解答题中都经常出现,常涉及不等式、函数、导数等知识,以及比较法、放缩法、构造法、数学归纳法等数学思想方法,对考查学生的知识能力和加大区分度都能起到很好的作用,因而倍受高考出题者的青睐。下面介绍高考中常用的几种方法。 一、求出数列通项式 利用这种方法,关键是把握好数列的递推关系式,熟悉求递推数列通项公式的方法,求出通项式后,再根据所给的不等关系求解。
二、利用数列的周期性 利用这种方法,关键是通过数列的递推关系式,得出该数列具有周期性,根据周期求出所需的某项,再根据所给的不等关系求解。
三、利用数学归纳法 这种方法通常用于证明题和比较大小的题,它要求对数学归纳法相当熟练。
四、利用作差(商)比较法 这种方法通常用于证明题和比较大小的题,它要求根据题目所给条件正确选取作差比较或作商比较的方法。
五、利用裂项求和法 利用这种方法,关键是根据数列的递推关系式,将所求式子转化为可裂项求和的形式,再根据所给的不等关系求解。 例5、已知二次函数 (Ⅰ)、求数列 (Ⅱ)、设 a=3 , b=-2, 所以 f(x)=3x2-2x. 又因为点 当n≥2时,an=Sn-Sn-1=(3n2-2n)- 当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 ( (Ⅱ)由(Ⅰ)得知 故Tn= 因此,要使 即m≥10,所以满足要求的最小正整数m为10。 六、利用累加(乘)法 利用这种方法,关键是根据数列的递推关系式,将所求式子转化为可累加求和或累乘求积的形式,再根据所给的不等关系求解。
利用这种方法,关键是根据数列的递推关系式,求出通项式进行放缩或将求式子转化为可放缩的形式,再根据放缩方法求解。 例7、已知数列{a 求证 : 证明:
八、利用构造法构造函数 利用这种方法,关键是根据数列的递推关系式所具备的函数特征构造函数,再根据函数思想或导数的方法求解。 例8、已知函数
证明: (I). 证明: (I).先用数学归纳法证明 ( = 1 \* roman i).当n=1时,由已知显然结论成立. ( = 2 \* roman ii).假设当n=k时结论成立,即
从而 由( = 1 \* roman i)、( = 2 \* roman ii)可知, 又因为 所以 (II).设函数 从而 所以g (x)在(0,1)上是增函数. 又g (x)在[0,1]上连续,且g (0)=0, 所以当 故 此文发表在《考试·高考数学》2008年5-6月刊 |
||
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

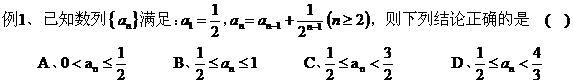
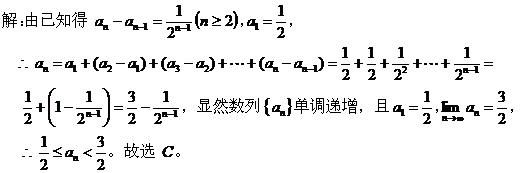
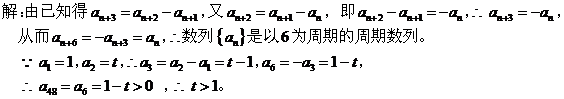
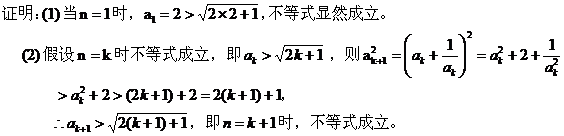
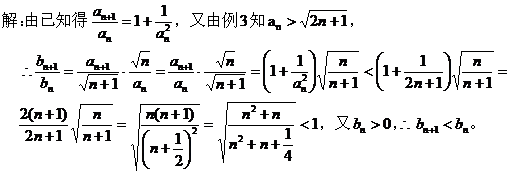
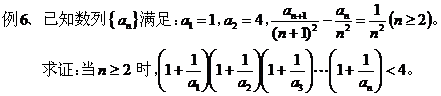
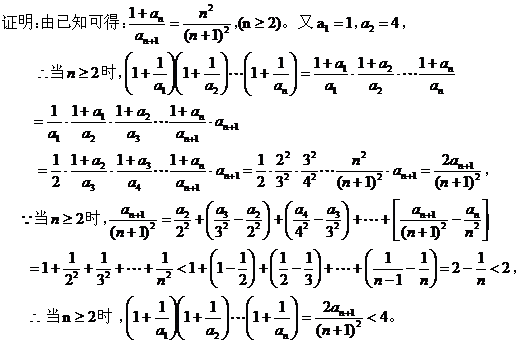 七、利用放缩法
七、利用放缩法