于真灵
一、深挖细查,突破解题的瓶颈.
例1 . 已知函数 有反函数,定义:若对给定的实数 有反函数,定义:若对给定的实数 ,函数 ,函数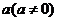 与 与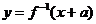 互为反函数,则称 互为反函数,则称 满足“ 满足“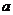 和性质”;若函数 和性质”;若函数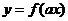 与 与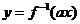 互为反函数,则称 互为反函数,则称 满足“ 满足“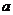 积性质”. 积性质”.
(1)判断函数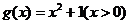 是否满足“1和性质”,并说明理由; 是否满足“1和性质”,并说明理由;
(2)求所有满足“2和性质”的一次函数;
(3)设函数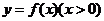 对任何 对任何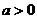 ,满足“ ,满足“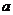 积性质”,求 积性质”,求 的表达式. 的表达式.
【简单解法】(1)因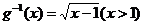 ,故 ,故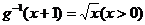 . .
而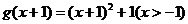 ,其反函数为 ,其反函数为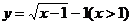 ,故 ,故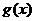 不满足“1和性质”. 不满足“1和性质”.
(2) )设函数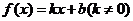 满足“2和性质”,则有 满足“2和性质”,则有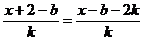 对 对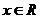 恒成立. 恒成立.
故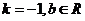 ,即所有求一次函数为 ,即所有求一次函数为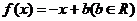 . .
(3) 设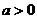 , ,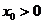 ,且点 ,且点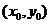 在 在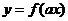 图象上,则 图象上,则 在函数 在函数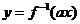 图象上,故 图象上,故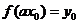 且 且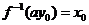 ,可得 ,可得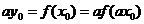 .令 .令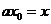 ,则 ,则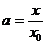 .故 .故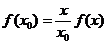 ,即 ,即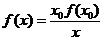 .综上, .综上,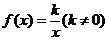 . .
【小 结】读懂并理解“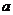 和性质” 与“ 和性质” 与“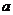 积性质”是解决这道题的关键.(3)问利用原函数与反函数的图象关于直线 积性质”是解决这道题的关键.(3)问利用原函数与反函数的图象关于直线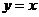 对称与“ 对称与“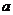 积性质”得到等式 积性质”得到等式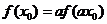 ,再通过换元 ,再通过换元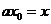 求得 求得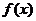 的解析式.创新题是目前高考与数学竞赛的常见题,挖掘题目中所给出的新概念、新定义、新运算、新性质等信息的本质,转化为用已掌握的数学知识来解决问题. 的解析式.创新题是目前高考与数学竞赛的常见题,挖掘题目中所给出的新概念、新定义、新运算、新性质等信息的本质,转化为用已掌握的数学知识来解决问题.
【突破训练】1.如果对任意一个三角形,只要它的三边长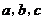 都在函数 都在函数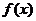 的定义域内,就有 的定义域内,就有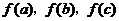 也是某个三角形的三边长,则称 也是某个三角形的三边长,则称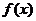 为“保三角形函数”. 为“保三角形函数”.
(1)判断下列函数是不是“保三角形函数”:① 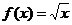 ;② ;②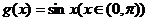 . .
(2)若函数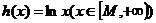 是保三角形函数,求 是保三角形函数,求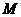 的最小值. 的最小值.
二、设而不求,架设解题的桥梁.
例2 . 已知直线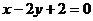 经过椭圆 经过椭圆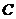 : : 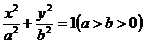 的左顶点 的左顶点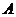 和上顶点 和上顶点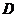 ,椭圆 ,椭圆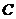 的右顶点为 的右顶点为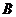 ,点 ,点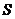 是椭圆 是椭圆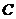 上位于 上位于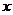 轴上方的动点,直线 轴上方的动点,直线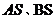 与直线 与直线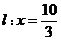 分别交于 分别交于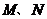 两点. 两点.
(1) 求椭圆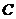 的方程; 的方程;
(2)求线段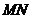 的长度的最小值; 的长度的最小值;
(3)当线段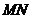 的长度取最小时,在椭圆 的长度取最小时,在椭圆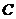 上是否存在这样的点 上是否存在这样的点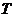 ,使得 ,使得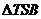 的面积为 的面积为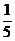 ?若存在,确定点 ?若存在,确定点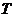 的个数;若不存在,说明理由. 的个数;若不存在,说明理由.
【简单解法1】 (1) 椭圆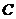 的方程为: 的方程为: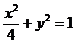 ; ;
(2)由于直线 的斜率 的斜率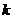 显然存在,且 显然存在,且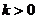 ,故可设直线 ,故可设直线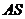 的方程为 的方程为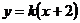 ,从而 ,从而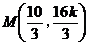 ,由 ,由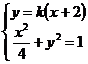 得 得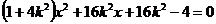 ,且它的一个根为 ,且它的一个根为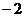 ,设 ,设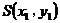 ,则 ,则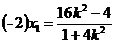 ,所以 ,所以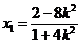 ,从而 ,从而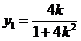 ,即 ,即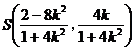 ;又 ;又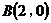 ,故 ,故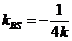 ,从而点 ,从而点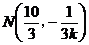 ,所以 ,所以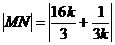 ,又 ,又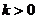 ,所以 ,所以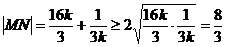 ,当且仅当 ,当且仅当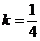 时,等号成立.所以当 时,等号成立.所以当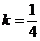 时,线段 时,线段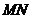 的长度取最小值 的长度取最小值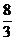 ,对应的点 ,对应的点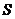 为 为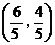 . .
(3)由(2)知,当线段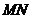 的长度取最小时, 的长度取最小时,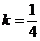 ,此时 ,此时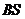 的方程为 的方程为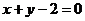 ,点 ,点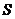 的为 的为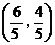 , ,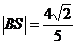 ;要使椭圆 ;要使椭圆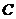 存在点 存在点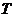 ,使得 ,使得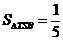 ,只需点 ,只需点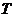 到直线 到直线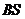 的距离为 的距离为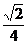 ,所以点 ,所以点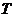 在平行于 在平行于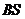 且与 且与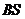 距离等于 距离等于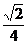 的直线 的直线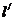 ,设直线 ,设直线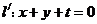 ,则由 ,则由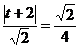 ,解得 ,解得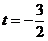 或 或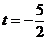 ,经检验,只有当 ,经检验,只有当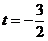 时,直线 时,直线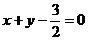 与椭圆有两个不同的交点.所以当线段 与椭圆有两个不同的交点.所以当线段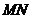 的长度取最小时,椭圆存在两个不同的点 的长度取最小时,椭圆存在两个不同的点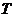 ,使 ,使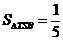 . .
【简单解法2】 (2)由椭圆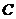 方程为: 方程为: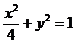 ,可设点 ,可设点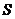 的坐标为 的坐标为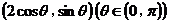 ,则直线 ,则直线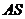 的方程为 的方程为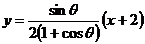 ,故点 ,故点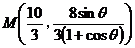 ,同理得 ,同理得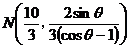 ,所以 ,所以 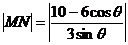 ,设 ,设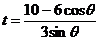 ,即 ,即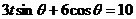 ,要使此式有意义,则 ,要使此式有意义,则
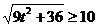 ,即 ,即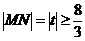 ,当 ,当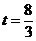 时, 时,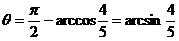 时,此时对应 的点 时,此时对应 的点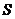 为 为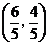 ;当 ;当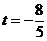 时, 时,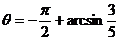 ,与 ,与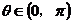 矛盾,故舍去. 矛盾,故舍去.
所以线段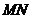 的长度取最小值 的长度取最小值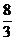 ,对应的点 ,对应的点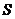 为 为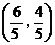 . .
【小 结】“设而不求”是联系解析几何与函数、方程、不等式等相关内容的纽带和桥梁,高考中许多解析几何题都能用“设而不求”解决,因此它是解决解析几何的金钥匙,本题中方法1设了点的坐标,由根与系数的关系得出;方法(2)设了点的参数坐标.常用的“设而不求”有:巧设相关点、巧设相关参数、巧设相关方程.
 【突破训练】2.设抛物线 【突破训练】2.设抛物线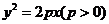 的焦点为 的焦点为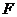 ,经过点 ,经过点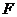 的直线交抛物线于 的直线交抛物线于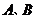 两点,点 两点,点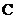 在抛物线的准线上,且 在抛物线的准线上,且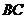 平行于 平行于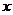 轴. 证明:直线 轴. 证明:直线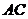 经过原点 经过原点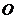 . .
三、执果索因,探究解题的方法.
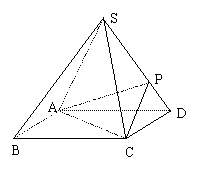
例3 .如图,四棱锥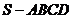 的底面是正方形,每条侧棱的长都 的底面是正方形,每条侧棱的长都
是底面边长的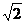 倍, 倍,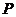 为侧棱 为侧棱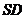 上的点. 上的点.
(1)求证: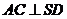 ; ;
(2) 若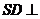 平面 平面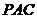 ,求二面角 ,求二面角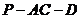 的大小; 的大小;
(3)在(2)的条件下,侧棱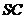 上是否存在一点 上是否存在一点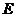 ,使得 ,使得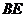 ∥平面 ∥平面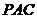 ?若存在,求 ?若存在,求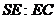 的值;若不存在,试说明理由. 的值;若不存在,试说明理由.
【简单解法】(1)连结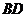 ,设 ,设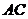 交 交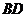 于 于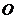 ,由题意知 ,由题意知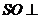 平面 平面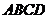 。以 。以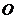 为坐标原点, 为坐标原点,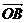 , ,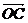 , ,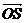 分别为 分别为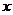 轴, 轴,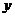 轴, 轴,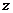 轴正方向,建立空间坐标系 轴正方向,建立空间坐标系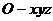 轴,设底面边长为 轴,设底面边长为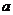 ,则高 ,则高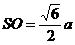 .于是, .于是,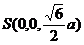 , ,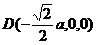 , ,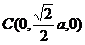 ,则 ,则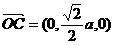 , ,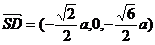 , ,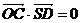 ,故 ,故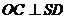 ,从而 ,从而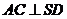 . .
(2)由题设知,平面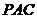 的一个法向量为 的一个法向量为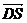 ,且 ,且 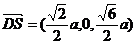 ,平面 ,平面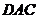 的一个法向量为 的一个法向量为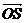 ,且 ,且 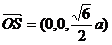 .设所求二面角为 .设所求二面角为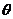 ,则 ,则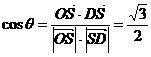 ,故所求二面角的大小为30o. ,故所求二面角的大小为30o.
(3)假设在棱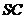 上存在一点 上存在一点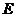 ,使得 ,使得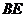 ∥平面 ∥平面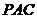 .由(2)知 .由(2)知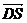 是平面 是平面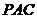 的一个法向量,且 的一个法向量,且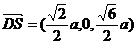 , ,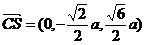 ,设 ,设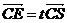 , ,
则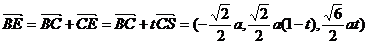 ,而 ,而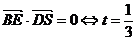 ,即当 ,即当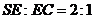 时, 时,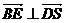 ,而 ,而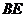 不在平面 不在平面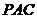 内,故 内,故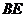 ∥平面 ∥平面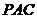 . .
【小 结】(3)从结论切入关键要解决向量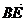 的表达式,使其满足“侧棱 的表达式,使其满足“侧棱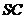 上是否存在一点 上是否存在一点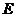 ,使得 ,使得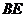 ∥平面 ∥平面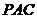 ”,先假设其存在,再转化为向量运算,降低了思维与运算的难度.探索型题通常是从结论入手,通过假设,逐步找到解题的方法. ”,先假设其存在,再转化为向量运算,降低了思维与运算的难度.探索型题通常是从结论入手,通过假设,逐步找到解题的方法.
【突破训练】3.在棱长为2的正方体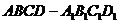 中, 中,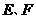 分别为 分别为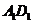 和 和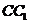 的中点. 的中点.
(1)求异面直线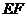 与 与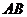 所成的角的余弦值; 所成的角的余弦值;
(2)在棱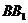 上是否存在一点 上是否存在一点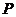 ,使得二面角 ,使得二面角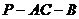 的大小为 的大小为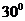 ?若存在,求出 ?若存在,求出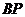 的长,若不存在,请说明理由. 的长,若不存在,请说明理由.
四、三角代换,转换解题的思维.
例4 .在数列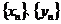 中, 中,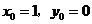 ,且满足关系式: ,且满足关系式: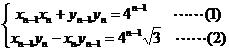 , ,
求: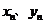 . .
【简单解法】将(1)和(2)两式平方后相加有: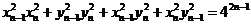 , ,
即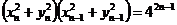 ,亦即 ,亦即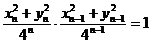 ……(3),而由 ……(3),而由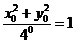 ,利用(3) ,利用(3)
得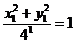 ,再据此利用(3)依次可推得: ,再据此利用(3)依次可推得: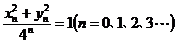 , ,
故有: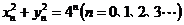 ,从而令 ,从而令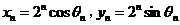 ,将其代入(1)和(2)得 ,将其代入(1)和(2)得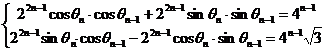 , ,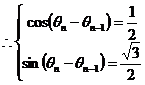 ,从而 ,从而
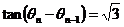 ,且 ,且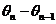 为第一象限的角,取 为第一象限的角,取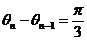 ,这说明 ,这说明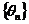 是以 是以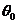 为首项、以 为首项、以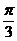 为公差的等差数列,即: 为公差的等差数列,即: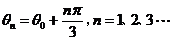 ,又由 ,又由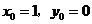 知 知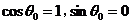 ,取 ,取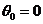 ,则 ,则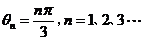 , ,
因此,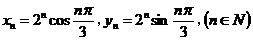 . .
【小 结】求递推数列的通项是求数列通项公式的一个难点,也是高考、尤其是高中数学竞赛的一个重点。通过对递推关系的一系列的变换,构成一个新的数列,是求解递推数列通项公式最常用的代数方法,但有时用代数法解这类题显得相当复杂,而利用三角知识可以很巧妙地解决这类问题。
【突破训练】4.设数列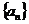 满足: 满足: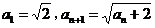 ,求通项公式 ,求通项公式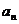 . .
【突破训练答案】1.(1) ① 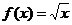 是保三角形函数;② 是保三角形函数;②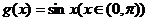 不是保三角形函数. (2)首先证明当 不是保三角形函数. (2)首先证明当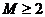 时, 时,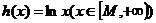 是保三角形函数,其次证明当 是保三角形函数,其次证明当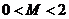 时, 时,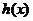 不是保三角形函数.综上知, 不是保三角形函数.综上知,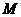 的最小值为2. 的最小值为2.
2.设过焦点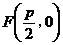 的直线 的直线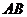 方程的方程为 方程的方程为 ,设 ,设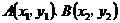 , ,
由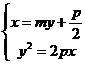 消去 消去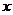 得 得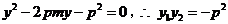 ,又 ,又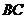 平行于 平行于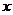 轴,且点 轴,且点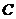 在准线上, 在准线上,
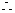 点 点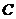 的坐标为 的坐标为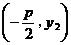 , ,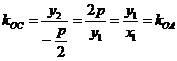 ,故 ,故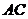 过原点. 过原点.
3.分别以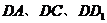 所在的直线为 所在的直线为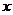 轴、 轴、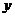 轴、 轴、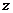 轴建立空间直角坐标系 轴建立空间直角坐标系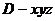 ,则 ,则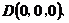 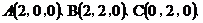 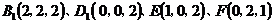 . .
(1)因为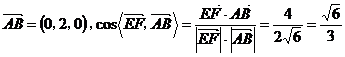 ,所以异面直线 ,所以异面直线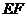 与 与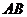 所成角的余弦值为 所成角的余弦值为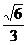 . .
(2)假设满足条件的点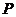 存在,可设点 存在,可设点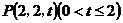 ,平面 ,平面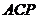 的一个法向量为 的一个法向量为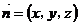 ,则 ,则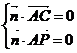 ,所以 ,所以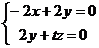 ,取 ,取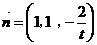 ,易知平面 ,易知平面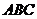 的一个法向量 的一个法向量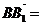 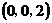 ,依题意知, ,依题意知,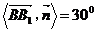 或 或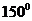 ,所以 ,所以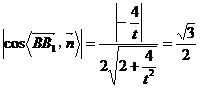 ,即 ,即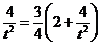 ,解得 ,解得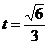 ,因为 ,因为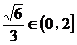 ,所以在棱 ,所以在棱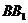 上存在一点 上存在一点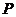 ,当 ,当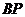 的长为 的长为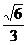 时,二面角 时,二面角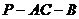 的大小为 的大小为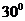 . .
4.不难用数学归纳法证明:对任意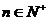 ,均有 ,均有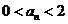 ,由此可令 ,由此可令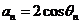 , ,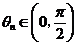 ,由 ,由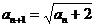 得: 得:
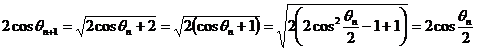 , ,
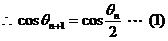 ,又 ,又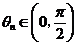 ,于是由(1)得 ,于是由(1)得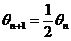 ,这说明 ,这说明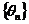 是以 是以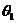 为首项、 为首项、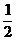 为公比的等比数列,故 为公比的等比数列,故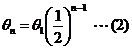 , ,
又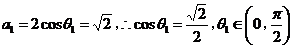 , ,
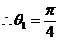 ,代入(2)得 ,代入(2)得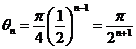 ,所以 ,所以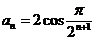 . .
此文发表在《高中生·高考指导》2010年11月下旬刊
|

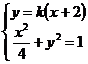 得
得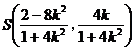 ;又
;又 【突破训练】2.设抛物线
【突破训练】2.设抛物线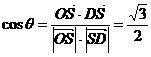 ,故所求二面角的大小为30o.
,故所求二面角的大小为30o.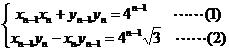 ,
,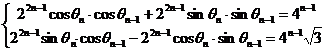 ,
,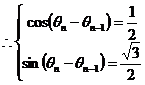 ,从而
,从而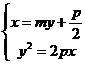 消去
消去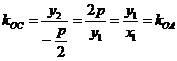 ,故
,故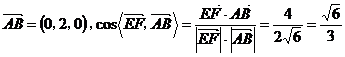 ,所以异面直线
,所以异面直线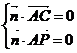 ,所以
,所以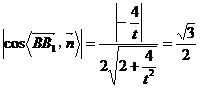 ,即
,即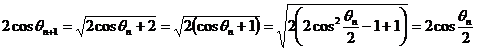 ,
,






