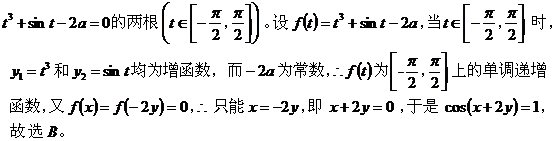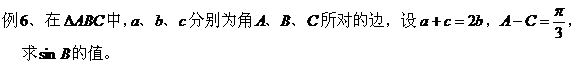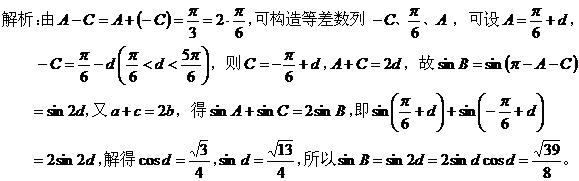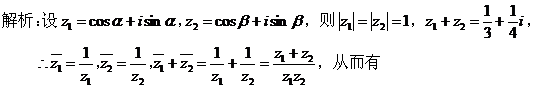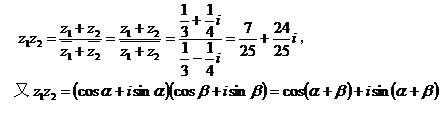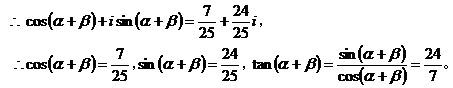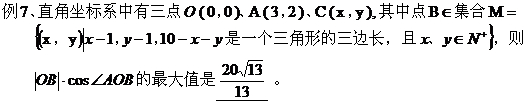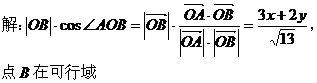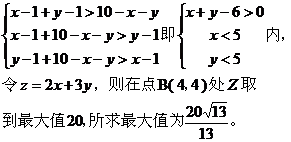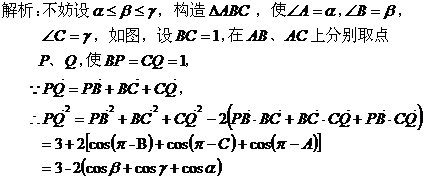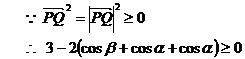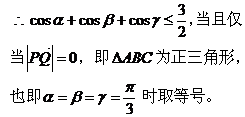构造数学模型 巧解三角问题 来源:绥宁一中校园网 作者:杨昌达 更新时间:2012-6-4 阅读:36074次 |
||
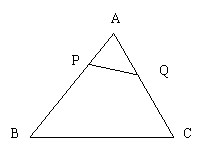
于真灵 三角问题包括三角公式、三角函数、解三角形等内容,是高考中重要考试内容之一,在解答三角问题中,运用的公式多、运算过程较繁锁、使用的方法多,但有些三角问题,如能从其所给条件中抓住其本质特征,构造数学模型,其解答过程就变得简单、快捷、准确。应用好构造思想解题的关键有二:一是要有明确的方向,即为了什么目的而构造;二是弄清条件的本质特点,以便重新进行逻辑组合。下面举例说明构造数学模型巧解三角问题。 1、构造平几模型
2、构造立几模型
解析:由于长方体一条对角线和它过同一个顶点的 三条棱所成角在余弦值的平方和为1,为此可 构造一个长方体
3、构造解几模型
4、构造函数模型
解析:已知条件可转化为
5、构造数列模型
6、构造复数模型
7、构造线性规划模型
8、构造向量模型
构造法解题是一种富有创造性的思维活动,一种数学形式的构造绝不是单一的思维方式,而是多种思维方式交叉、联系、融汇在一起共同作用的结果。三角问题的解法很多,但能抓住其本质特征,采用构造法,能快捷、准确地将问题解决。 此文发表在《语数外学习·高考数学》2008年8月中旬刊 |
||
推荐使用Chorme或国内浏览器的“极(快)速模式”浏览 【后台管理】 主办单位:绥宁县第一中学
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667
联系电话:0739-7611972 湘ICP备14001922号-1 地址:湖南省绥宁县长铺镇工业街10号 湘教QS7_201311_001667

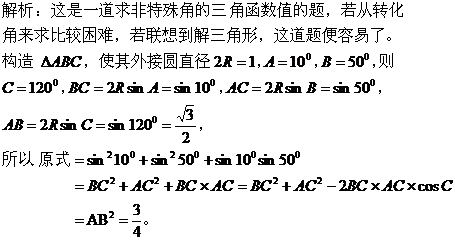

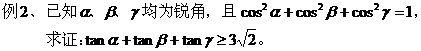
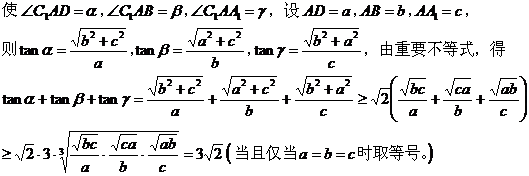
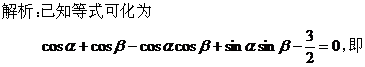
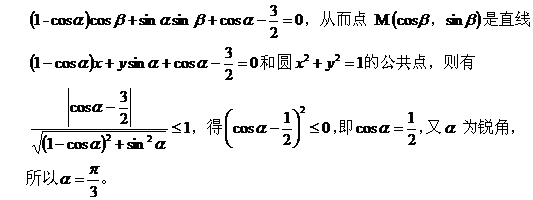
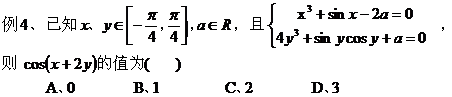
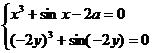 ,从而
,从而